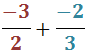Tema 4: Operaciones combinadas de sumas y restas con fracciones
Sumar y restar fracciones
En esta página explicamos cómo sumar y restar fracciones (con denominador igual y con denominador distinto) y resolvemos 35 ejercicios de sumas y restas.
Contenido de esta página:
- Introducción
- Fracciones con denominador común
- Fracciones con distinto denominador
- Suma de dos fracciones negativas
- Fracciones con signos negativos
- 35 ejercicios resueltos de sumas y restas de fracciones
Páginas relacionadas
- Concepto de fracción y su lectura
- Simplificar fracciones
- Equivalencia entre fracciones
- Fracción irreductible
- Multiplicar y dividir fracciones
- Fracción generatriz
- Fracción mixta
- Porcentajes y fracciones
- Operaciones con fracciones
- Fracción irreductible y fracciones equivalentes
- Ejercicios interactivos de fracciones
- Calculadoras de fracciones
Otras páginas:
1. Introducción
Como las fracciones son números, es lógico que se puedan sumar y restar. Estas operaciones son fáciles de calcular, aunque se realizan de forma distinta según si los denominadores de las fracciones son iguales o distintos.
Recordad que el numerador es el número sobre la raya de la fracción y el denominador es el que esta debajo de la raya. Por ejemplo,

2. Fracciones con denominador común
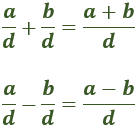
La suma de dos fracciones con el mismo denominador se calcula sumando sus numeradores. El denominador se mantiene.
Por ejemplo, sumamos las fracciones \(4/7\) y \(3/7\):
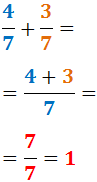
Representación gráfica:
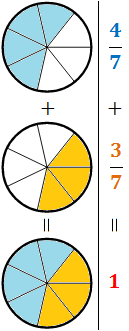
Análogamente,
La resta de dos fracciones con el mismo denominador se calcula restando sus numeradores. El denominador se mantiene.
Por ejemplo, restamos las fracciones \(4/7\) y \(3/7\):
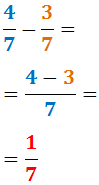
Representación gráfica:
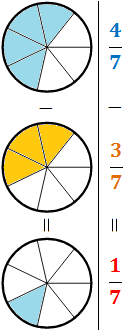
3. Fracciones con denominador distinto
Cuando el denominador es distinto, tenemos que realizar más operaciones. Vamos a explicar dos métodos:
- Método 1: utilizar el mcm de los denominadores.
- Método 2: multiplicar en las fracciones por los denominadores.
Recordad que una fracción es equivalente (o igual) a otra fracción si ambas representan al mismo número. Por ejemplo, las fracciones \(1/2\) y \(2/4\) son equivalentes porque representan al número \(0.5\).
Para sumar y restar fracciones con denominador distinto, buscamos dos fracciones que sean equivalentes a éstas y que tengan el mismo denominador.
Por ejemplo, queremos sumar las fracciones \(3/4\) y \(1/2\), que tienen denominador distinto:
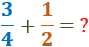
Como la fracción \(1/2\) es equivalente a la fracción \(2/4\), podemos intercambiarlas para tener una suma de fracciones con el mismo denominador:
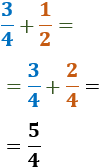
Para restar las fracciones, hacemos lo mismo.
Cómo encontrar fracciones equivalentes con el mismo denominador:
- El nuevo denominador (de ambas fracciones) es el mínimo común múltiplo (mcm) de los denominadores. Recordad que el mcm es el producto de los factores comunes y no comunes al mayor exponente.
- El nuevo numerador de cada fracción se calcula dividiendo el nuevo denominador por el antiguo y multiplicando el resultado por el antiguo numerador.
Por ejemplo, vamos a calcular la suma de las fracciones \(4/7\) y \(3/14\):
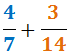
- Calculamos el mcm de los denominadores (7 y 14):
La descomposición de 14 en números primos es:
$$ 14 = 7 \cdot 2 $$
El número 7 no se puede descomponer en primos ya que él mismo es un primo.
Los factores que aparecen en las descomposiciones son 2 y 7, ambos con exponente 1.
El mínimo común múltiplo es el producto de todos los factores al mayor exponente. Por tanto, el mínimo común múltiplo de 7 y 14 es
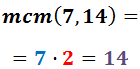
- En el denominador de cada fracción escribimos el mínimo común múltiplo obtenido:
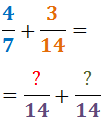
- El denominador inicial de la primera fracción era 7 y el numerador inicial era 4. Calculamos el nuevo numerador:
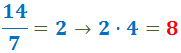
El denominador inicial de la segunda fracción era 14 y el numerador inicial era 3. Calculamos el nuevo numerador:
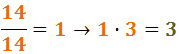
Por tanto, tenemos ya la suma de fracciones con igual denominador:
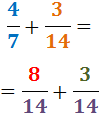
Como los denominadores son iguales, sumamos los numeradores:
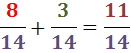
Representación gráfica:
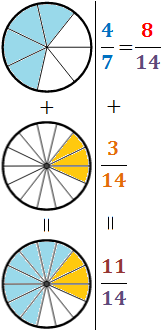
Este método consiste en multiplicar el numerador y el denominador de cada fracción por el denominador de la otra fracción. Esto hace que ambas fracciones tengan el mismo denominador.
Por ejemplo,
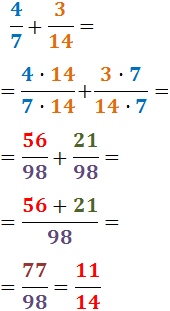
Recomendamos el método del mcm (mínimo común múltiplo) ya que en el que segundo:
- tenemos que calcular productos y sumas de números que normalmente son grandes y
- los resultados son fracciones que se tienen que simplificar.
4. Suma de dos fracciones negativas
Recordad la suma de dos números negativos. Por ejemplo,
$$ (-2)+(-3) = -2-3 =-5$$
En el caso de fracciones negativas, se procede del mismo modo.
Ejemplo (denominador común):
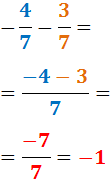
Ejemplo (distinto denominador):
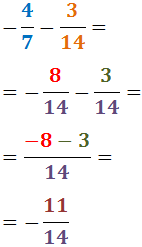
5. Fracciones con signos negativos
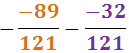
Una fracción puede tener un signo negativo en el numerador y/o en el denominador y/o delante de la fracción:
- Si sólo tiene un signo negativo, la fracción es negativa:
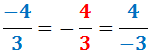
- Si tiene dos signos negativos, la fracción es positiva:
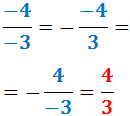
- Si los signos son positivos, la fracción es positiva (normalmente, no encontraremos fracciones escritas de este modo ya que el signo positivo suele reservarse para indicar una suma):
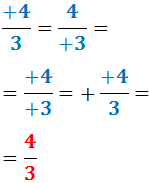
Los casos anteriores son el resultado de aplicar la regla de los signos (del producto).
6. Ejercicios resueltos
Parte I
Calcular las siguientes sumas y restas de fracciones con denominador común y simplificar, si es posible, el resultado.
Ejercicio 1
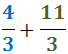
Ejercicio 2
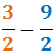
Ejercicio 3
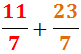
Ejercicio 4
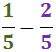
Ejercicio 5
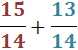
Ejercicio 6
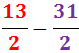
Ejercicio 7
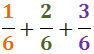
Ejercicio 8
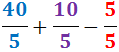
Ejercicio 9
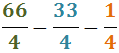
Ejercicio 10
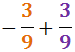
Ejercicio 11
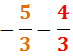
Ejercicio 12
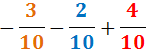
Ejercicio 13
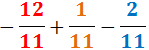
Ejercicio 14
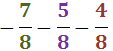
Ejercicio 15
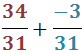
Ejercicio 16
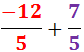
Ejercicio 17
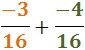
Ejercicio 18
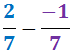
Ejercicio 19
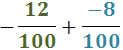
Ejercicio 20
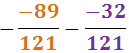
Parte II
Calcular las siguientes sumas y restas de fracciones con distinto denominador y simplificar, si es posible, el resultado.
Ejercicio 21
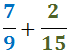
Ejercicio 22
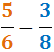
Ejercicio 23
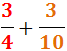
Ejercicio 24
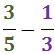
Ejercicio 25
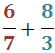
Ejercicio 26
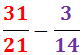
Ejercicio 27
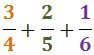
Ejercicio 28
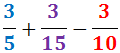
Ejercicio 29
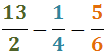
Ejercicio 30
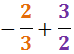
Ejercicio 31
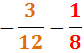
Ejercicio 32
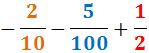
Ejercicio 33
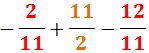
Ejercicio 34
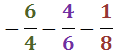
Ejercicio 35