Tema 2: Dominio y recorrido de una función
Dominio y recorrido de una función
En esta página explicamos el concepto de dominio, codominio y recorrido de una función de una variable y resolvemos 13 ejercicios.
1. Definiciones
Una función, f, relaciona los elementos de dos conjuntos, A y B. Normalmente, se escribe f:A→B.
A es el dominio de f y B es el codominio. Normalmente, se denota al dominio de f por Dom(f).
A cada elemento a del dominio A, la función f le asigna un único elemento b del codominio B. Lo denotamos por
f(a)=b
Se dice que b es la imagen de a y que a es la antiimagen de b.
El conjunto de todas las imágenes del dominio se denomina conjunto imagen o recorrido de f. Normalmente, se escribe como Im(f).
La imagen de f es un conjunto contenido en el codominio B.
2. Algunos ejemplos
Ejemplo 1
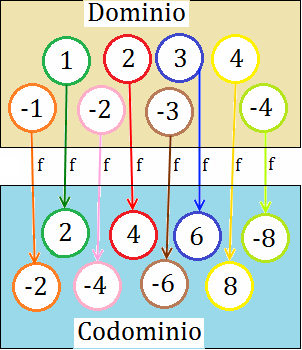
Dominio: es el conjunto formado por los números 1, -1, 2, -2, 3, -3, 4 y -4.
Normalmente, el dominio de las funciones que veremos es el conjunto de los números reales: R.
Codominio: es el conjunto formado por los números 2, -2, 4, -4, 6, -6, 8 y -8.
La imagen de 1 es 2 y la imagen de -3 es -6, es decir, f(1)=2 y f(−3)=−6.
La antiimagen de 8 es 4 y la antiimagen de -4 es -2, es decir, f−1(8)=4 y f−1(−4)=−2.
Imagen: coincide con el codominio.
La función f relaciona cada número del dominio con su doble (lo multiplica por dos). Podemos escribir la función f como
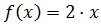
Así, si sustituimos x por un elemento del dominio, tenemos su imagen. Por ejemplo,
- La imagen de 1 es f(1)=2⋅1=2.
- La imagen de -1 es f(−1)=2⋅(−1)=−2.
- La imagen de 2 es f(2)=2⋅2=4.
- La imagen de -2 es f(−2)=2⋅(−2)=−4.
Ejemplo 2
Sea la función f:R→R dada por f(x)=x2. Calculamos algunas imágenes:
- f(0)=02=0
- f(1)=12=1
- f(−1)=(−1)2=1
- f(2)=22=4
- f(−2)=(−2)2=4
- f(3)=32=9
- f(−3)=(−3)2=9
Dominio:
El dominio de f es el conjunto de los reales: Dom(f)=R.
Imagen:
La imagen de f es el conjunto de los reales no negativos, Im(f)=R+, porque el cuadrado de un número siempre es no negativo. Además, todos los reales no negativos tienen antiimagen.
Por ejemplo, el número 7 tiene dos antiimágenes: +7 y −7 ya que
f(7)=(7)2=7
f(−7)=(−7)2=7
Una elemento b del codominio puede tener más de una antiimagen, pero un elemento a del dominio sólo tiene una imagen.
3. Gráfica
La gráfica de una función f es el conjunto de los puntos (x,f(x)) tal que x es del dominio de f:
Γ(f)={(x,f(x)):x∈Dom(f)}
Por ejemplo, la gráfica de f(x)=x2 es
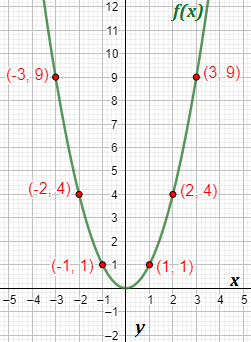
Hemos representado algunos puntos que vimos en el ejemplo anterior.
4. Ejercicios resueltos
Nota previa: la forma más rápida de hallar el recorrido de una función es observando su gráfica. Sin embargo, vamos a intentar deducirlo de forma razonada. Para ello, podemos ayudarnos de la monotonía (creciente o decreciente) y de límites.
Calcular el dominio y el recorrido de las siguientes funciones:
Ejercicio 1
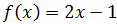
Ejercicio 2
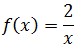
Ejercicio 3
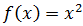
Ejercicio 4
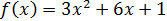
Ejercicio 5
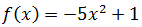
Ejercicio 6
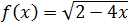
Ejercicio 7
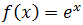
Ejercicio 8
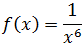
Ejercicio 9
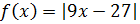
Ejercicio 10
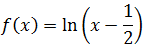
Ejercicio 11
![función parte entera de x, f(x) = E[x] Explicamos los conceptos de dominio, codominio y recorrido (o imagen) de una función y resolvemos ejercicios. Función racional, raíz cuadrada, función definida a trozos, polinómica, exponencial, valor absoluto, logarítmica, etc. Matemáticas. Análisis de una variable real.](https://www.matesfacil.com/ESO/dominio/dominio11.png)
Ejercicio 12
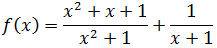
Ejercicio 13

