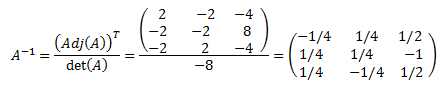Tema 1: Matriz de 3 × 3 y sus operaciones
Matrices: concepto, suma, producto, transpuesta, determinante, adjunta e inversa.
1. Concepto de Matriz y operaciones básicas
1.1. Concepto
Una matriz es un conjunto ordenado de números. Los números están ordenados por filas y por columnas.
La dimensión de una matriz es m x n, siendo m el número de filas y n el número de columnas.
Cuando m = n, se dice que la matriz es una matriz cuadrada de dimensión m.
Ejemplo de una matriz:
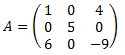
Esta matriz tiene 3 filas y 3 columnas. Por tanto, es una matriz de dimensión 3×3. Es una matriz cuadrada de dimensión 3.
Cada número de la matriz ocupa una posición determinada por la columna y la fila a las que pertenece. La posición de un número de la matriz es (i,j), siendo i la fila y j la columna.
En el ejemplo, las posiciones (1,2), (2,1), (3,2) y (2,3) son 0’s. El número 4 está en la posición (1,3), y el número -9 está en la posición (3,3).
1.2. Suma de matrices
Si dos matrices tienen la misma dimensión, el resultado de sumarlas es la matriz que en la posición (i,j) tiene la suma de los números de la posición (i,j) de las dos matrices.
Ejemplo de una suma de matrices:
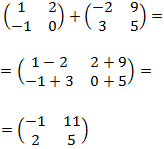
1.3. Multiplicación de un escalar por una matriz
El producto de un número α por una matriz A es la matriz que resulta al multiplicar todos los elementos de A por el número α.
Ejemplo:

1.3. Matriz transpuesta
Dada una matriz A de dimensión m x n, se define la matriz transpuesta de A como la matriz que resulta al escribir las filas de A como columnas. Esta matriz tiene dimensión n x m.
Ejemplo de matriz transpuesta:
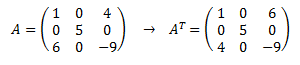
(como la matriz es cuadrada, la dimensión de la transpuesta de A es la misma que la de A.)
1.4. Matrices especiales
Se llama matriz diagonal a cualquier matriz tal que los elementos de la posición (i,j) son 0’s si i≠j.
Ejemplo de matriz diagonal:

Una matriz cuadrada de dimensión n se dice que es la matriz identidad de dimensión n si es diagonal y en las posiciones (i,i) tiene 1’s:
Ejemplo de matrices identidad:
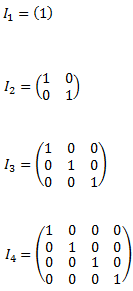
Más información:
- Concepto de matriz
- Ejemplos de sumas de matrices
- Matrices con nombre (diagonal, triangular, Hessenberg, diagonalmente dominante, simétrica, definida positiva…)
2. Producto de matrices
2.1. Definición del producto
Para poder calcular el producto A·B de la matriz A se requiere que el número de columnas de A coincida con el número de filas de B.
Si la dimensión de A es m x n y la dimensión de B es n x p, el producto A·B es una matriz de dimensión m x p.
El elemento de la posición (i,j) de la matriz A·B es el resultado de multiplicar la fila i de A por la columna j de B.
Ejemplo de producto de matrices:
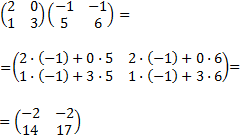
- El elemento de la posición (1,1) de la matriz A·B es el resultado de multiplicar la fila 1 de A por la columna 1 de B:
(2,0)·(-1,5) = 2·(-1)+0·5 = -2
- El elemento de la posición (1,2) de la matriz A·B es el resultado de multiplicar la fila 1 de A por la columna 2 de B:
(2,0)·(-1,6) = 2·(-1) +0·6 = -2
- El elemento de la posición (2,1) de la matriz A·B es el resultado de multiplicar la fila 2 de A por la columna 1 de B:
(1,3)(-1,5) = 1·(-1) +3·5 = 14
- El elemento de la posición (2,2) de la matriz A·B es el resultado de multiplicar la fila 2 de A por la columna 2 de B:
(1,3)·(-1,6) = 1·(-1)+3·6 = 17
EL producto de matrices NO es conmutativo. Es decir, puede ocurrir que A·B ≠ B·A.
La matriz identidad de dimensión adecuada es el neutro del producto de matrices. Es decir, si la matriz A es de dimensión m x n, entonces
Im·A = A = A·In
2.2. Matriz inversa
Si A es una matriz cuadrada de dimensión n, se denomina matriz inversa de A (y se representa mediante A-1) a la matriz de dimensión n, en caso de existir, que cumple
A·A-1 = In = A-1·A
Ejemplo:
La matriz inversa de
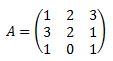
Es la matriz
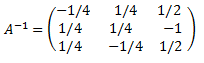
Antes de ver cómo calcular la inversa, necesitamos explicar el determinante y la matriz adjunta de una matriz.
Más información:
- Ejemplos del producto de matrices
- Matriz inversa (teoría)
- Cálculo de la matriz inversa (por adjunción)
- Potencias de matrices
3. Determinante de una matriz
El determinante es una función definida sobre matrices cuadradas. El determinante de una matriz A se representa por det(A), DET(A) o bien |A|.
Vamos a ver cómo calcularlo según la dimensión de la matriz:
Dimensión 1:
Si la matriz es de dimensión 1, es de la forma A = (a). Entonces, su determinante es det(A) = a. Por ejemplo, el determinante de la matriz A = (-3) es |A| = -3.
Dimensión 2:
La matriz es de la forma

Su determinante es
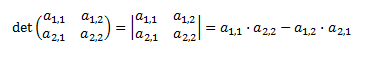
Por ejemplo,
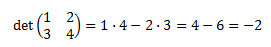
Dimensión 3:
La matriz es de la forma

Su determinante es
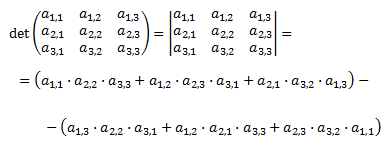
(regla de Sarrus).
Por ejemplo,
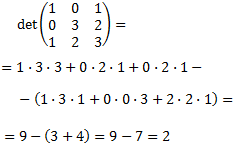
Dimensión mayor que 3:
No hay una regla (fácil) para calcular su determinante. En estos casos, aplicaremos el desarrollo del determinante por Laplace. El desarrollo del determinante de por la fila i de la matriz A de dimensión n es
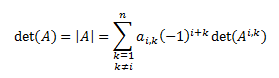
La matriz Ai,j es la matriz resultante al quitar la fila i y la columna j de A.
El desarrollo puede aplicarse también a matrices de dimensión menor que o igual que 3, por ejemplo,
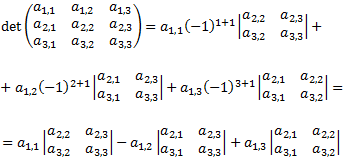
Más información:
4. Adjunta de una matriz
Dada una matriz cuadrada A = (ai,j), donde ai,j representa el número de la posición fila i y columna j de A, se define el adjunto (i,j) de A como
adi,j = (-1)i+j· det( Ai,j )
donde la matriz Ai,j es la matriz resultante al quitar la fila i y la columna j de A.
Se llamada matriz adjunta de A, adj(A), a la matriz (de la misma dimensión que A) que tiene en la posición (i,j) el adjunto adi,j de la matriz A.
Ejemplo:
Calculamos los adjuntos de la matriz:
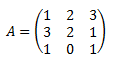
Éstos son:
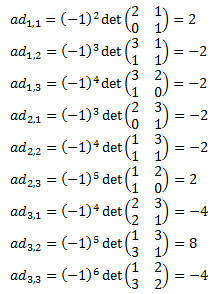
Por tanto, la matriz adjunta es:
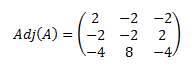
5. Cálculo de la matriz inversa
Si A es una matriz cuadrada y su determinante es distinto de 0, entonces existe su matriz inversa, A-1.
Un forma de calcular esta matriz es a partir de su matriz adjunta, Adj(A):
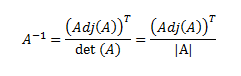
(T indica transpuesta).
Ejemplo:
En el ejemplo anterior, la matriz adjunta calculada es:
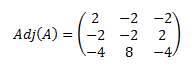
El determinante de la matriz A es
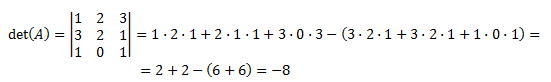
Por tanto, la inversa de A es