Tema 10: Producto cartesiano. Aplicaciones
Producto cartesiano
Para entender la idea de producto cartesiano debemos saber que se trata de una operación entre dos conjuntos , de tal modo que se forma otro conjunto con todos los pares ordenados posibles.
Por ejemplo, dados los conjuntos A = {1, 2, 3, 4} y B = { a , b }, su producto cartesiano es:
A × B = {(1, a ), (1, b ), (2, a ), (2, b ), (3, a ), (3, b ), (4, a ), (4, b )}
Los elementos de A x B son pares ordenados. Cada par que se forma con un elemento del conjunto A y uno del conjunto B, en ese orden, recibe el nombre de par ordenado. Sus elementos se colocan entre paréntesis, separados por coma.
Entonces:
El poducto cartesiano de dos conjuntos cualesquiera A y B, será un nuevo conjunto, identificado como A x B , y consistirá de un conjunto de parejas ordenadas, (x, y), donde x pertenece al conjunto A e y pertenece al conjunto B.
Como ejemplo:
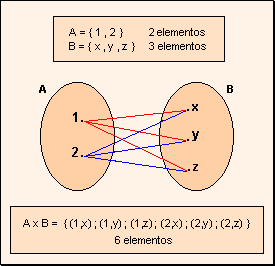
También podríamos decir que un par ordenado es una colección de dos objetos distinguidos como primero y segundo , y se denota como ( a , b ), donde a es el “primer elemento” y b el “segundo elemento”.
El producto cartesiano recibe su nombre de René Descartes , cuya formulación de la geometría analítica dio origen a este concepto.
Representación gráfica de un producto cartesiano
Los pares ordenados representarán puntos coordenado en el plano cartesiano , tomando como primera coordenada un elemento del primer conjunto, y como segunda coordenada a un elemento del segundo conjunto, independientemente que sean números u otras entidades.
