Tema 2: Máximo común divisor
Máximo Común Divisor (M.C.D.)
El máximo común divisor (MCD) de dos o más número natural o enteros (no números con decimales) es el número más grande que les divide.
Para descubrir cuáles son los números que les divide existen dos formas: la forma larga y la forma corta. Esto lo explicaremos a través de un ejemplo. Ejemplo:
Forma larga
Máximo común divisor (MCD) de 10 y 20:
Divisor de 20: 1, 2, 4, 5, 10 y 20.
Divisor de 10: 1, 2, 5 y 10.
Importante: los divisores se sacan dividiendo, es decir, todo número que dividido por el número que estamos analizando de 0 en el resto. Por ejemplo:
0 2
4 1
– 6 No sería divisor de 10 porque el resto da 4 y tiene que ser 0.
Una vez sabido que los divisores de 10 y de 20 son:
Divisor de 20: 1, 2, 4, 5, 10 y 20.
Divisor de 10: 1, 2, 5 y 10.
Vamos a ver cuáles son los números que coinciden que son:
Divisor de 20: 1, 2, 4, 5, 10 y 20.
Divisor de 10: 1, 2, 5 y 10.
Divisores de 10 y 20 son: 1, 2, 5 y 10.
El máximo común divisor sería el 10 porque es el número más grande que, a su vez, es divisor de ambos número (10 y 20).
Forma corta
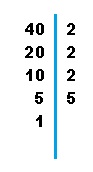
Para número más grandes es más fácil hacer una descomposición en factores primos. Esta descomposición la empezamos siempre con el número más pequeño divisible del número que analizamos. Por ejemplo, para descubrir el máximo común divisor de 40 y 60. Escribimos el número que vamos a descomponer a la derecha (en este caso el 40) y seguidamente trazamos una recta vertical. Será detrás de esta donde colocaremos los factores primos empezando por el más pequeño. Haremos lo mismo con el 60.
|
|
En este paso hemos dividido 40:2=20. Ahora buscaremos el mínimo divisor de 20 que es 2 y hacemos lo mismo 20:2= 10. Y seguiremos haciendo lo mismo con todos los anteriores. |
¡Truco! Si quieres saber si has hecho bien la descomposición de ffactores primos se puede comprobar multiplicando. Empezando por abajo, multiplicas el último número de la izquierda (multiplicando) con el último de la derecha (multiplicador), el resultado debe ser el número de arriba del multiplicando.
Ejemplo:
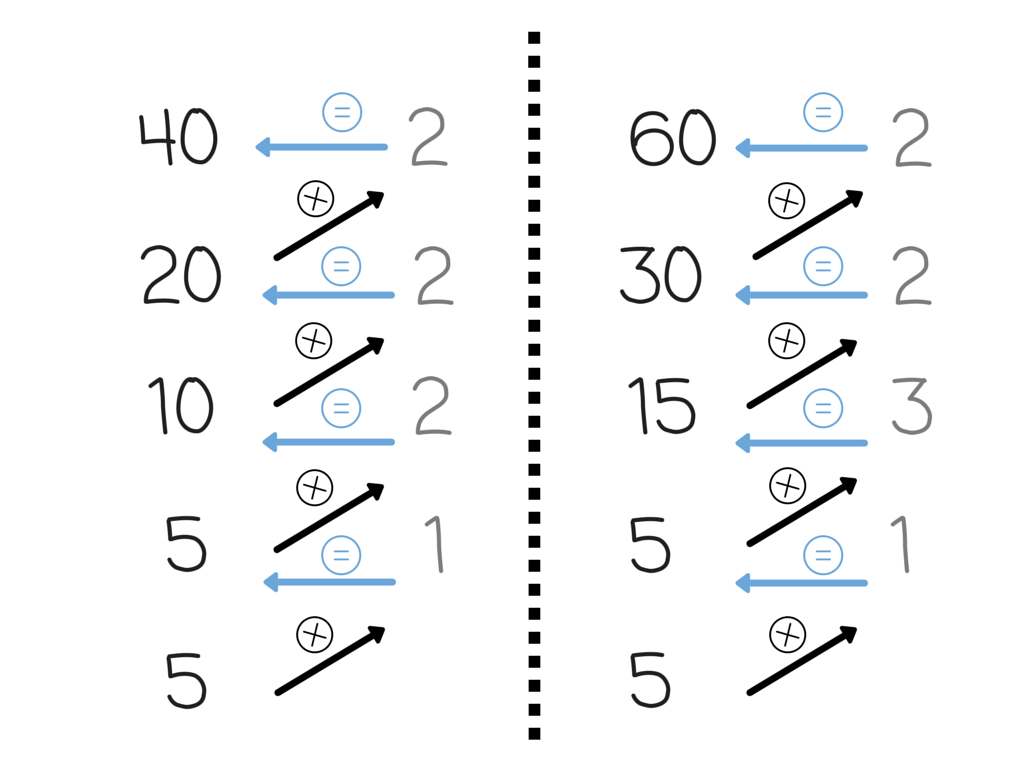 |
El último número es el 5 (multiplicando) el multiplicador será el 1 y el resultado es el 5. Lo mismo pasa si 5 (multiplicando) lo multiplicas por 2 (multiplicador) es igual a 10. |
Una vez descompuesto el número 40 sabemos que 40 es divisor de:
|
|
MCD de 40 = 2x2x2x5 |
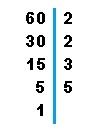
El mismo proceso seguiremos con el número 60:
Una vez fragmentados ambo
|
|
MCD de 60 = 2x2x5x5 |
Una vez fragmentados ambos números vemos que:
Los divisores de 40 son: 2x2x2x5
Los divisores de 60 son: 2x2x3x5
Observamos cuales son los números que se repiten (los que estan en negrita) y los multiplicamos:
2x2x5= 20
El máximo común divisor de 40 y 60 es 20
Vídeo explicativo
Resumen o chuleta de máximo común divisor
El máximo común divisor de dos o más números es el número, más grande posible, que permite dividir a esos números.
Para calcularlo: De los números que vayas a sacar el máximo común divisor, se ponen uno debajo del otro, se sacan todos los divisores de los dos números y el máximo que se repita es el máximo común divisor (M.C.D.)
Ejemplo: Sacar el M.C.D. de 20 y 10:
20 = 1, 2, 4, 5, 10, 20
10= 1, 2, 5, 10
Esto sirve para números pequeños. Pero para números grandes hay otra manera: la descomposición de factores.
Forma rápida de calcular el Máximo común Divisor (M.C.D.).
Ejemplo: Sacar el M. C. D. de 40 y 60:
1. Tienes que saber las reglas divisibilidad. Haces la descomposición de factores poniendo números primos. Por ejemplo: para 40, en la tabla de abajo, se va descomponiendo en 2, 2, 2 y 5.
2º De los resultados, se cogen los números repetidos de menor exponente y se multiplican. Ese es el M.C.D.
M.C.D. = 2 x 2 x 5
M.C.D. de 40 = 2 x 2 x 2 x 5
M.C.D. de 60 = 2 x 2 x 3 x 5