Tema 9: Cuerpos de revolución: características y clasificación
Cuerpos de Revolución
Un cuerpo de revolución es aquel que se origina al girar una figura plana alrededor de un eje. Las caras de un cuerpo de revolución son curvas.
Podemos distinguir:
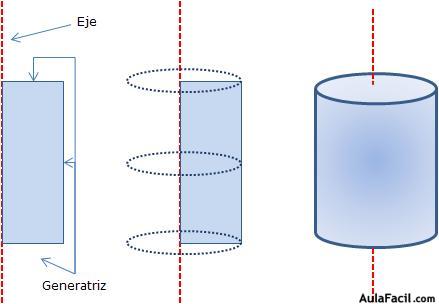
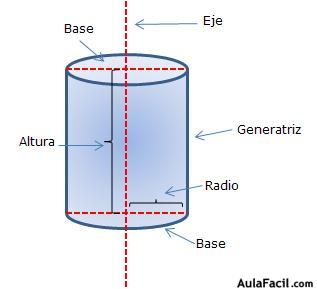
Eje: recta alrededor de la cual gira la figura plana para general el cuerpo de revolución.
Generatriz: son los límites exteriores de la figura plana.
Entre los cuerpos de revolución destacamos: la esfera, el cilindro y el cono.
a) Esfera:
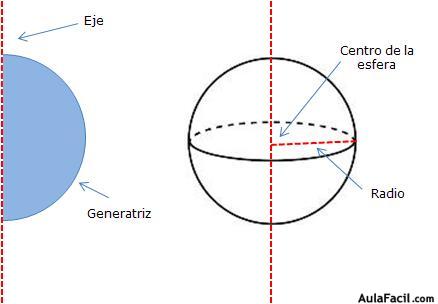
La esfera se genera al girar una semicircunferencia alrededor de un eje
En la esfera todos los puntos están a la misma distancia de su centro. El segmento que une cada punto de la esfera con el centro se denomina radio.
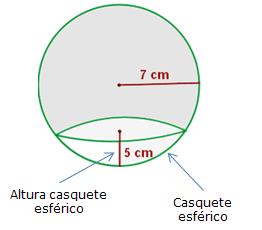
Si se corta una esfera con un plano, dejando fuera el centro de la esfera, se obtiene un casquete esférico.
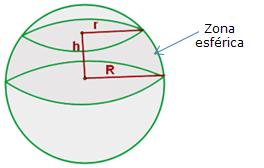
Si se corta una esfera con dos planos paralelos, la porción de esfera delimitada se denomina zona esférica.
b) Cilindro: tiene dos bases paralelas con forma de círculo y una cara lateral curva. Se genera al girar un rectángulo alrededor de un eje.
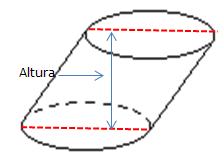
c) Cilindro oblicuo: resulta de cortar oblicuamente un cilindro recto con dos planos paralelos.
Las bases de un cilindro oblicuo son elipses. Su altura es la distancia entre los planos que contienen las bases.
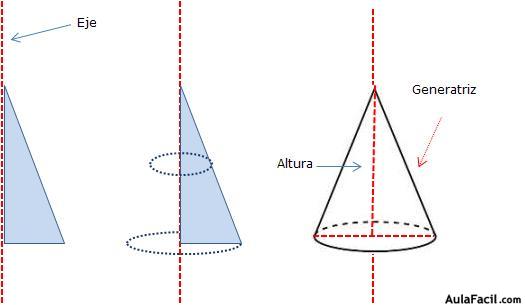
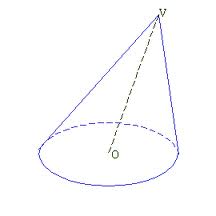
d) Cono: tiene una sola base en forma de círculo y una cara lateral curva que finaliza en un punto llamado vértice o cúspide.
Esta figura se obtiene girando un triángulo rectángulo alrededor un eje.
La generatriz es el segmento que va desde cualquier punto de la circunferencia de la base al vértice.
e) Cono Inclinado
Se obtiene cortando un cono de forma oblicua con un plano. La base de un cono inclinado no es circular sino que tiene forma de elipse.
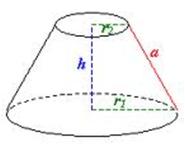
f) Tronco de cono
Es una figura que se obtiene al cortar un cono con un plano horizontal