Tema 1: Sistema de ecuaciones lineales con dos incógnitas. Método gráfico de resolución.
Método gráfico para resolver sistemas de ecuaciones. Ejercicios resueltos.
A continuación te voy a explicar en qué consiste el método gráfico para resolver sistemas de ecuaciones con dos incógnitas. Lo veremos con ejercicios resueltos paso a paso.
¡Empezamos!
Si has llegado hasta aquí es porque seguramente necesitas clases de matemáticas. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Qué es el método gráfico de un sistema de ecuaciones
El método gráfico, como su nombre indica, se utiliza para resolver sistemas de ecuaciones con dos incógnitas de una forma gráfica.
Para entender este método, debes tener muy claro cómo es la ecuación de una recta. La ecuación de una recta en su forma explícita tiene esta forma:

Donde m y n son variables.
Si te das cuenta, la ecuación de una recta es una ecuación con dos incógnitas, x e y, tal y como tenemos en un sistema de ecuaciones.
Por tanto, cada una de las ecuaciones que forman un sistema corresponde a la ecuación de una recta, por lo que podemos representar cada una de ellas en los ejes cartesianos y el punto de corte de ambas rectas corresponderá a la solución del sistema de ecuaciones.
Pasos para resolver un sistema de ecuaciones por el método gráfico
Los pasos para resolver un sistema de ecuaciones por el método gráfico son los siguientes:
- Despejamos la incógnita «y» en cada una de las ecuaciones
- Representamos cada una de las rectas en los ejes de coordenadas
- Las coordenadas del punto de corte de ambas rectas, será la solución del sistema de ecuaciones.
Vamos a verlo con un ejemplo paso a paso para que te quede todo mucho más claro.
Ejemplo de un sistema de ecuaciones resuelto por el método gráfico
Tenemos el siguiente sistema de ecuaciones, el cual lo vamos a resolver por el método gráfico:

En primer lugar, en la primera ecuación:

Despejamos «y»:

Ya tenemos la «y» despejada, aunque su forma no es igual la ecuación explícita de una recta, ya que en el segundo término tenemos una fracción y la ecuación de una recta tiene dos términos:

Si separamos el segundo miembro en dos términos, manteniendo el denominador vemos que nos quedan dos términos, como en la ecuación de la recta:

Este paso no es necesario hacerlo. Tan sólo lo he hecho para que veas que efectivamente tenemos la ecuación de una recta.
Una vez tenemos la «y» despejada, vamos a representar la recta en los ejes cartesianos. Si necesitas ayuda para saber cómo representar una recta, en esta lección lo tienes explicado paso a paso.
Para representar una recta, necesitamos dos puntos de la misma. Para obtenerlos, vamos a elegir dos valores de x al azar y obtendremos su correspondiente valor de «y». Yo voy a elegir los valores x=0 y x=1 (pero repito que pueden ser cualquiera).
Para x=0, calculamos su correspondiente valor de «y», sustituyendo x por 0 en la expresión donde despejamos la «y»:

Hacemos lo mismo para x=1:

Con los valores obtenidos, vamos creando la tabla de valores:

Una vez tenemos ambos puntos, los representamos en los ejes de coordenadas. Ten en cuenta que en 5/3 es igual a 1,66 para que te sea más fácil ubicarlo en los ejes:

Para representar la recta, sólo tenemos que unir ambos puntos y alargar al recta por ambos extremos:

Ya tenemos la recta de la primera ecuación representada. Ahora vamos a hacer lo mismo con la segunda ecuación:

Despejamos «y»:

Damos dos valores a x para obtener sus correspondientes valores de «y». En este caso, también voy a elegir x=0 y x=1.
Para x=0, su valor de «y» es:

Para x=1, su valor de «y» es:

Ordenamos los resultados en una tabla de valores:

Ahora, en los mismos ejes donde ya tenemos representada la primera recta, representamos los puntos de la segunda recta:
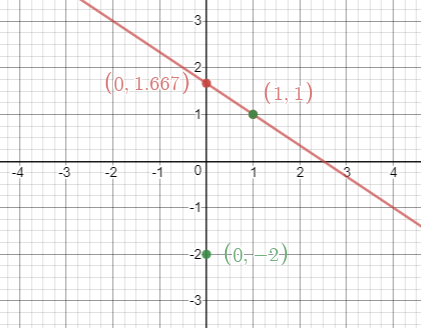
Y volvemos a unir ambos puntos para obtener la representación gráfica de la segunda recta, alargándola por los dos extremos:

El punto de corte de ambas rectas corresponde con la solución del sistema de ecuaciones. En este caso, se ve claramente que el punto de corte es (1,1), por lo que la solución del sistema es x=1, y=1, que son las coordenadas del punto de corte.
Ejercicios resueltos de sistema de ecuaciones por el método gráfico
Vamos a resolver más sistemas de ecuaciones para que practiques con el método gráfico. Verás que el procedimiento a seguir siempre es el mismo.
Ejercicio resuelto 1
Resuelve el siguiente sistema de ecuaciones por el método gráfico:

En la primera ecuación:

Despejamos «y»:

Vamos a representar esta ecuación en los ejes cartesianos y para ello vamos a obtener dos puntos que pertenezcan a la recta. Lo hacemos eligiendo dos valores cualquiera de x y calculando su correspondiente valor de «y».
Elijo los valores x=0 y x=1 y obtengo el valor de «y» en cada caso sustituyendo la x por su valor en cada caso.
Para x=0, su valor de «y» es:

Para x=1, su valor de «y» es:

Creamos la tabla de valores con los valores de x y de «y»:

Representamos ambos puntos en los ejes y después trazamos la recta que pasa por ambos puntos:

Una vez tenemos la primera recta representada, vamos a hacer los mismo con la segunda ecuación:

Despejamos «y»:

Volvemos a dar dos valores a x para obtener sus correspondientes valores de «y», que también voy a elegir x=0 y x=1.
Para x=0, su valor de «y» es:

Para x=1, su valor de «y» es:

Configuramos la tabla de valores:

En los mismos ejes donde representamos la primera recta, representamos los puntos de la segunda ecuación y trazamos su recta:
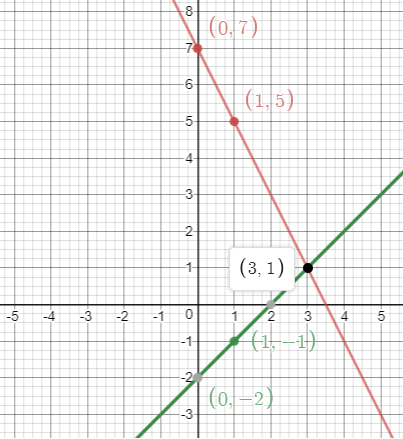
El punto de corte de ambas rectas es la solución del sistema de ecuaciones. En este caso, el punto de corte es (3,1), por lo que la solución del sistema es x=3, y=1.
Ejercicio resuelto 2
Resuelve el siguiente sistema de ecuaciones por el método gráfico:

Empezamos despejando «y» en la primera ecuación


Obtenemos dos puntos de la recta, dándole valores cualquiera a la x. Le doy x=0 y x=1.
Para x=0 su valor de «y» es:

Para x=1 su valor de «y» es:

Los ordenamos en una tabla de valores:

Y representamos la recta en los ejes de coordenadas:
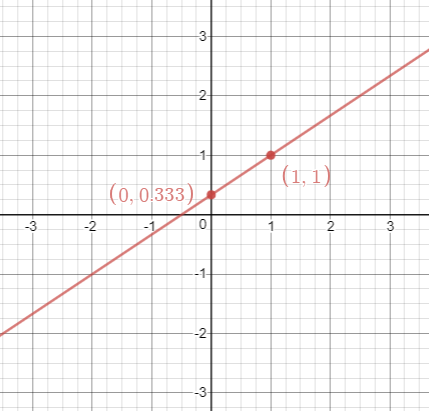
Con la segunda ecuación hacemos lo mismo:

Despejamos «y»:

Obtenemos dos puntos de la recta dando dos valores a x, que volverán a ser x=0 y x=1. Sustituimos la x por cada valor y obtenemos el valor correspondiente de «y»:


Creamos la tabla de valores:

Y representamos la recta:
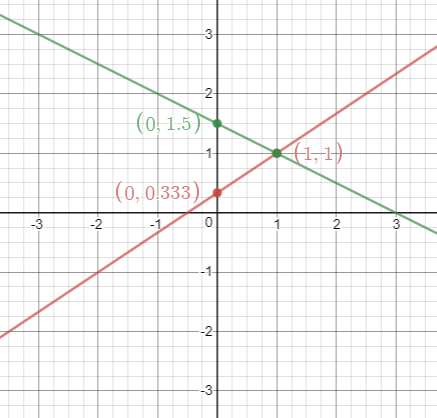
El punto de corte de ambas rectas es la solución del sistema de ecuaciones. En este caso, el punto de corte es (1,1), por lo que la solución del sistema es x=1, y=1.
Como ves, el procedimiento para resolver sistemas de dos ecuaciones con dos incógnitas por el método gráfico es siempre el mismo.
El método gráfico es el menos utilizado de todos los métodos de resolución de sistemas de ecuaciones, ya que por una lado es más lento el tener que representar cada una de las rectas y por otro, si las coordenadas del punto de corte no son números enteros, la solución es menos precisa que con el resto de métodos.
También debes saber que no siempre vas a obtener un punto de corte. Eso va a depender del tipo de sistema de dos ecuaciones.
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
