Tema 4: Herramientas TIC para estadística. Uso del programa GeoGebra.
Hoja de Cálculo Estadística Básica 
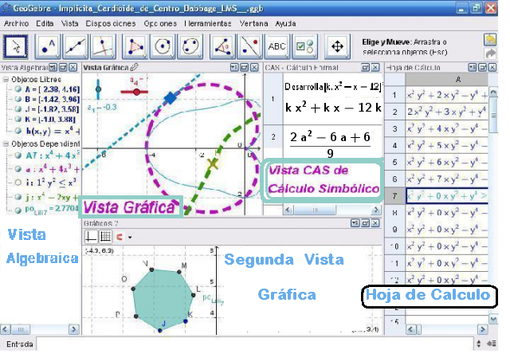
- Esta multiplicidad permite apreciar los objetos matemáticos en tres registros diferentes: gráfico en la
 Vista Gráfica (como en el caso de puntos, gráficos de funciones), algebraico en la Vista Algebraica (como coordenadas de puntos, ecuaciones) y en celdas de una Hoja de Cálculo.
Vista Gráfica (como en el caso de puntos, gráficos de funciones), algebraico en la Vista Algebraica (como coordenadas de puntos, ecuaciones) y en celdas de una Hoja de Cálculo.
Cada registro del mismo objeto se vincula dinámicamente a las demás en una adaptación automática y recíproca que asimila los cambios producidos en cualquiera de ellas, más allá de cuál fuera la que lo creara originalmente.
- Además, a partir de cierta versión en adelante, está disponible una Vista CAS que respalda el desarrollo de ciertos cálculos, numéricos y simbólicos y las principales operaciones algebraicas así como el acceso a derivadas, integrales, resolución de ecuaciones y/o ecuaciones diferenciales y variedad de otras.
Entradas a las Celdas de la Hoja de Cálculo
Toda celda de la Hoja de Cálculo de GeoGebra tiene una denominación específica que permite dirigirse a cada una. Por ejemplo, la celda en la fila 1 de la columna A se llama A1.
Registro en la Hoja de Cálculo
En las celdas de una hoja de cálculo, pueden ingresarse tanto números como cualquier otro tipo de objeto tratado por GeoGebra (sean coordenadas de puntos, funciones, comandos, textos) en general y, desde ya, matemáticos – específicamente geométrico – en particular. Cuando corresponde, también aparece de inmediato, en la ![]() Vista Gráfica, la representación del objeto ingresado en la celda, cuyo nombre coincide con el de la celda de la hoja de cálculo a partir de la cual fue creado (por ejemplo: A5, C1, D3′, etc.).
Vista Gráfica, la representación del objeto ingresado en la celda, cuyo nombre coincide con el de la celda de la hoja de cálculo a partir de la cual fue creado (por ejemplo: A5, C1, D3′, etc.).
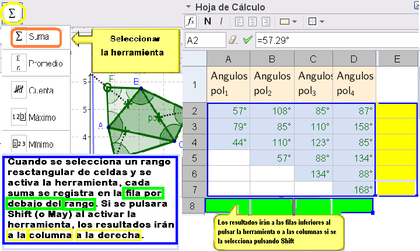
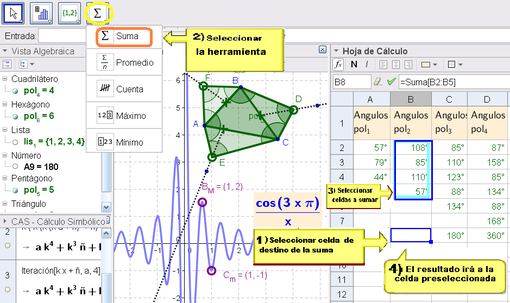
Operaciones Calculadas por Herramientas de la Hoja
Como en toda Hoja de Cálculo es posible operar con ese específico estilo algebraico que caracteriza esos ambientes, para, por ejemplo, llevar adelante simas o promedios de un rango de celdas.La figura previa y la siguiente ilustran la secuencia de maniobras para sumar varias celdas con esta
Preparando la Interfaz de Uso y la Barra de Herramientas
Sea desde el Menú Vista, el de Apariencias o desde la Barra de Estilo, se puede determinar qué partes de la interfaz van a exponerse y cuáles no, seleccionando la opción correspondiente (particularmente, la de la Hoja de Cálculo en el Menú Vista así como la Barra de Entrada…).
Preparativos
- Abrir una Nueva Ventana de GeoGebra desde el Menú Archivo.
- Seleccionar, en el Menú Apariencias, la de la Hoja de Cálculo y Gráficos.
Pasos de Construcción
| 1 | Crear un deslizador con un intervalo acorde al fijado por omisión y un incremento de 1.
|
|
| 2 | Crear un punto A anotando A = (a, 2a) en la Barra de Entrada.
|
|
| 3 | Exponer el rótulo del punto A en la |
|
| 4 | Cambiar el valor del deslizador a para ensayar con diferentes posiciones del punto A. | |
| 5 | Usar las herramientas Desplaza Vista Gráfica, así como las de Aproximar y Alejar para ajustar la zona visible de la |
|
| 6 | Registrar las coordenadas para las diferentes posiciones del punto A en la hoja de cálculo:
|
Desafíos
Desafíos 1:Examinar el patrón de valores de y en la columna B
Una vez establecido el escenario de exploración, se puede plantear como desafío:
- procurar develar el patrón que se registra en la columna B, creado por la ordenada del punto A en cada una de las posiciones que ocupa
- anticipar la gráfica de la eventual función que se ajuste a las diferentes posiciones del punto A
- controlar la coincidencia que se pudiera corroborar entre la gráfica de la función que se ingresara en la Barra de Entrada – como f(x) = 2 x, por ejemplo- y la del trazo que cruza por todos los puntos.
Desafíos 2: Crear un nuevo problema
Basta con cambiar la ordenada del punto A parar crear un nuevo problema:
- Un clic derecho (MacOS: Ctrl –clic) sobre el punto A para seleccionar Propiedades de Objeto… del Menú Contextual emergente.
- En la pestañaBásico, cambiar la ordenada del punto A en el campo de texto Definición a, por ejemplo, a^2.
- Apelar a las demás pestañas para cambiar el color, o la medida (en Estilo) de A.
- Cerrar el Cuadro de Propiedades al terminar de realizar los cambios deseados,
- Reiterar los pasos anotados en las instrucciones previas para registrar las coordenadas de la nuevas posiciones de A en la Hoja de Cálculo
Nota: Si no se eliminan los valores previos en las columnas A y B, GeoGebra automáticamente emplea las dos siguientes columnas vacías (como las C y D) para tal registro de los nuevos valores de las coordenadas x e y respectivamente.
Copia Relativa y Ecuaciones Lineales
Preparativos
- Abrir una Nueva Ventana de GeoGebra desde el Menú Archivo.
- Seleccionar, en el Menú Apariencias, la de la Hoja de Cálculo y Gráficos.
Pasos de Construcción
| 1 | Seleccionar la herramienta de Desplaza Vista Gráfica para arrastrar el origen del sistema de coordenadas hacia el vértice inferior izquierdo de la |
|
| 2 | En la Hoja de Cálculo, basta un clic en la celda A1 para anotar el punto de coordenadas (0, 0). | |
| 3 | En A2, (1, 1). | |
| 4 | Exponer los rótulos de sendos puntos en la |
|
| 5 | Copia relativa de las coordenadas de los puntos incorporados en otras celdas de la columna A:
|
|
| 6 | Emplear la herramienta que Desplaza la Vista Gráfica así como la del Aproximar y las del Alejar para ajustar la zona de trabajo en la |
Desafío Nro. 1: Examinar la secuencia de las coordenadas del punto
¿Qué secuencia de números se crea cuando se aplica la «copia relativa» de la hoja de cálculos de GeoGebra tal como se ha descripto en las secciones previas?
Desafío Nro. 2: Hallando la ecuación que se ajusta
Anticipar qué ecuación podría establecer un gráfico a través de todos los puntos de esta secuencia. Anotarla en la Barra de Entrada para controlar la suposición.
Desafíos 3: Crear un nuevo problema
Basta con cambiar las coordenadas de los puntos iniciales parar crear un nuevo problema:
Versión 1
- Cambiar las coordenadas de los puntos iniciales con un doble clic en la celda A2 de la Hoja de Cálculo para pasar a anotar, por ejemplo, (1, 2) y confirmar este valor pulsando Enter (o Intro en algunos teclados).
Versión 2
- Cambiar los puntos iniciales en la
 Vista Gráfica, con la Herramienta de Elige y Mueve que permita desplazar el punto A a una posición diferente en el sistema de coordenadas. Inmediatamente, todos los puntos dependientes se adaptarán dinámicamente a estos cambios tanto en la Hoja de Cálculo como en la Gráfica.
Vista Gráfica, con la Herramienta de Elige y Mueve que permita desplazar el punto A a una posición diferente en el sistema de coordenadas. Inmediatamente, todos los puntos dependientes se adaptarán dinámicamente a estos cambios tanto en la Hoja de Cálculo como en la Gráfica.
Para delimitar las coordenadas de los puntos a valores enteros, es conveniente establecer, en la Barra de Estilo de la
Indagando Regularidades Numéricas
La propuesta será vincular el cambio en la longitud de las aristas de un cubo con su modificación de superficie.
Preparativos
- Abrir una Nueva Ventana de GeoGebra desde el Menú Archivo.
- Seleccionar, en el Menú Apariencias, la de la Hoja de Cálculo y Gráficos.
- En el Menú de Opciones o en la Barra de Estilo de la
 Vista Gráfica, establecer Solo los Nuevos Puntos para el Rotulado .
Vista Gráfica, establecer Solo los Nuevos Puntos para el Rotulado .
Pasos de Construcción
Crear un Gráfico de Dispersión a partir de los Datos
| 1 | Anotar los siguientes números en las celdas de la columna A de la Hola de Cálculo, A1: 1 A2: 2 | |
| 2 | Iluminar y seleccionar las celdas A1 y A2 y arrastrarlas hasta la A20 para que se concrete la copia de los valores correspondientes a la secuencia creciente de longitud de aristas.
|
|
| 3 | En la columna B, anotar los valores de la superficie de la caja cúbica según la arista, que no son sino los de las seis caras cuadradas que tienen por longitud de lado, la de la arista.
|
|
| 4 | Seleccionar la celda B1 para copiar la fórmula que contiene hasta la B20. | |
| 5 | Crear un gráfico de dispersión:
Nota: Los valores de las columnas A y B determinan, respectivamente, la abscisa y la ordenada de los puntos en cuestión.
|
|
| 6 | Emplear las herramientas adecuadas para hacer visible el conjunto de puntos en la |
Indagar el Patrón de Resultados en la Columna B
| 7 | En la celda C2, se puede ingresar la fórmula = B2-B1 para calcular la diferencia entre los dos valores sucesivos de superficie.
|
|
| 8 | Seleccionar la celda C2 y proceder a la copia relativa de la fórmula hasta C20. | |
| 9 | En la celda D3, anotar la fórmula = C3-C2 para calcular la diferencia entre las dos sucesivas diferencias. | |
| 10 | Seleccionar la celda D3 y proceder a la copia relativa de la fórmula hasta D20. |
Desafío 1
Examinar la secuencia de números en las columnas C y D para realizar una conjetura respecto de la función polinómica que cruzaría por el conjunto de puntos involucrado y que, por otra parte, resulte consistente con la determinación de la superficie del cubo.
- ¿Será posible determinar…
- … el grado de tal polinomio para investigar la secuencia de diferencias generadas en las columnas C y D?
- … los coeficientes de tal polinomio para indagar en la secuencia de diferencias registradas en las columnas C y D?
- … si estos resultados conservarían esta regularidad para valores en la columna A no necesariamente enteros sucesivos (como, por ejemplo, 1, 3, 5,…)?
- … dar justificaciones para cada respuesta?
Controlando las Conjeturas
| 11 | Crear un par de deslizadores…
|
|
| 12 | Anotar el polinomio f(x) = a * x^n para crear un polinomio de grado n con coeficiente a.
Nota: Tanto el grado como el coeficiente se pueden modificar a expensas de los correspondientes deslizadores.
|
|
| 13 | Cambiar el valor de los deslizadores a y n para corroborar las conjeturas que se hubieran elaborado y controlar que el polinomio cruce por todos los puntos registrados en la |
Ajustes en la Construcción
| 14 | Insertar la ecuación del polinomio como un texto dinámico en la
Nota: GeoGebra automáticamente adoptará la sintaxis necesaria para manejar dinámicamente este texto.
|
|
| 15 | Incluir una Casilla de Control para Mostrar / Ocultar Objetos que permita mostrar / ocultar de la ecuación polinómica.
|
|
| 16 | Activar la Herramienta de Elige y Mueve para verificar la operatoria correcta de la casilla recién creada. | |
| 17 | Abrir el Cuadro de Propiedades para:
|
Desafío 2
- Llevar adelante los ensayos necesarios para controlar si esta modalidad de indagación conceptual sobre la secuencias de diferencias de los valores de las dos funciones sucesivas opera para todos los polinomios f(x) = a x^n.
-
 Atención:
Atención:
Se puede ingresar una fórmula – recordando empezar con el signo = – en la celda B1 para realizar una copia relativa hasta la celda B20 para crear una lista de valores de función.
- Considerar qué modificaciones son necesarias, tanto en la Hoja de Cálculo como en la
 Vista Gráfica, para determinar la constante de polinomios como este f(x) = a x^n + b.
Vista Gráfica, para determinar la constante de polinomios como este f(x) = a x^n + b.
Mejor Ajuste Lineal
Preparativos
- Abrir una Nueva Ventana de GeoGebra desde el Menú Archivo.
- Seleccionar, en el Menú Apariencias, la de la Hoja de Cálculo y Gráficos.
- En el Menú de Opciones establecer Solo los Nuevos Puntos para el Rotulado .
Pasos de Construcción
| 1 | Anotar los siguientes números en las celdas de la hoja de cálculo de la columna A:
A1: 1 A2: 5 A3: 2 A4: 8 A5: -2 |
|
| 2 | En las celdas de la columna B:
B1: -1 B2: 2 B3: 3 B4: 4 B5: 1 |
|
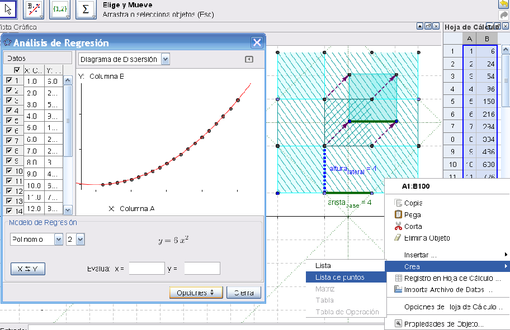
| 3 | Usar la herramientas de Análisis de Regresión de Dos Variables para crear la función que se ajusta a esos datos puntuales. Iluminar las celdas y seleccionar con un clic la herramienta. | |
| 4 | Procurar dar con la función que mejor se ajusta a los puntos seleccionando diferentes Modelos de Regresión. |
Desafío Nro. 1: Examinar los modelos de regresión
Indagar por qué algunos modelos no operan con los puntos ingresados, anotando diferentes puntos y ensayando con la ![]() Herramienta de Análisis de Regresión de Dos Variables nuevamente.
Herramienta de Análisis de Regresión de Dos Variables nuevamente.
Desafío Nro. 2: Regresión Polinomial
Seleccionar el Modelo de Regresión Polinomial para observar qué le sucede a la función cuando se le cambia el orden polinomial.
Importando Datos desde otras Hojas de Cálculo
- Seleccionar y copiar los daos que se quieran importar (por ejemplo, empleando los atajos de teclas usuales Ctrl + C para copiar los datos en el portapapeles del equipo de trabajo).
- Abrir la ventana de GeoGebra para exponer la Hoja de Cálculo.
- Seleccionar con un clic, la celda de la planilla que contiene el dato del primero valor.
- Pegar el dato desde el portapapeles del equipo de trabajo en la Hoja de Cálculo de GeoGebra. Para hacerlo, se puede volver a emplear los atajos de tecla – en este caso Ctrl + V o clic derecho (MacOS: Ctrl – clic) en la celda iluminada y seleccionar Pega desde el menú contextual emergente.
Explorando las Estadísticas Básicas
Planteo del Problema
Si en un examen a 25 estudiantes se les consulta sobre la dificultad involucrada pidiéndoles que califiquen con un valor de 1 («muy fácil») a 5 («muy difícil»).
- 4 estudiantes lo calificaron «muy fácil» (1)
- 6, como «fácil» (2)
- otros 6, como «difícil» (4)
- 1 como «muy difícil» (5)
- El resto opinó que el grado de dificultad era «apropiado» (3).
Desafío Nro. 1: Creando un histograma
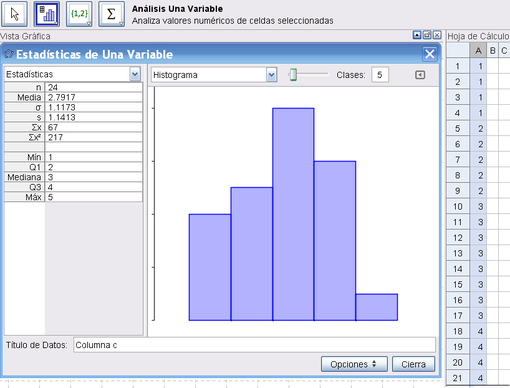
Ingresar los datos en la planilla de GeoGebra para crear u histograma que ilustre estos datos.
- Emplear la herramienta de Herramienta de Análisis de una variable para crear un histograma.
- Cambiar el deslizador Clases en la ventana emergente para controlar el número de barras que se exponen en el histograma.
- Mejorar el histograma ajustando las clases manualmente y cambiando los parámetros de inicio y de ancho.
Desafío Nro. 2: Determinando la media y la mediana
- Anticipar la media y la mediana de los datos involucrados.
- Comparar la solución controlando la tabla a la izquierda de la ventana de Estadísticas de Análisis de una variable.