Tema 7: Características de cuadrados y rectángulos
RECTÁNGULO

Un rectángulo es un polígono con cuatro lados (cuadrilátero) siendo éstos iguales dos a dos. Además, sus cuatro ángulos interiores son rectos (de 90º).
Elementos y propiedades del rectángulo

- Lados: tiene cuatro lados, siendo cada lado igual a su opuesto (a y b), es decir, dos a dos.
- Ángulos: sus cuatro ángulos (α) son iguales y rectos de 90º (π/2 radianes). Los ángulos interiores, como en todo cuadrilátero, suman 360º (2π radianes).
- Diagonales: las diagonales son segmentos que unen los vértices opuestos. Tiene dos diagonales (D1 y D2) iguales y que se cortan en el centro del rectángulo.
- Ejes de simetría: son líneas imaginarias que dividen el rectángulo en dos partes simétricas respecto a dicho eje. Tiene dos ejes de simetría (E1, E2) paralelos a los lados a y b y pasan por el centro del rectángulo.
Un caso particular de rectángulo es el cuadrado, cuando todos los lados son iguales (a=b).
Diagonal del rectángulo

La diagonal del rectángulo (D) se puede calcular a partir de la longitud de los lados diferentes (a y b). La fórmula para calcular la diagonal es:

Ésta fórmula se obtiene directamente de la ley del paralelogramo.
También podría obtenerse también a partir del teorema de Pitágoras, ya que dos lados (a y b) consecutivos del rectángulo y la diagonal forman un triángulo rectángulo.
La diagonal se obtiene también en función del área del rectángulo (A) y uno de sus lados:
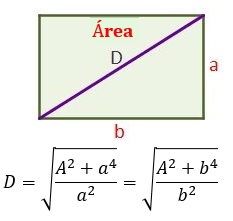
Conociendo el área y el ángulo que forman sus diagonales, se puede hallar la diagonal de éste:

El ángulo agudo γ de las diagonales es el doble del ángulo β que forma una diagonal con el lado mayor:

Área del rectángulo
El área del rectángulo se calcula a partir de los dos lados diferentes (a y b). Es el producto de los dos lados contiguos del rectángulo.


Esta fórmula también podría obtenerse de la fórmula del área del paralelogramo. Si la base del rectángulo es uno de sus lados (en este caso b) , la altura relativa a la base será el lado a, y aplicando la fórmula anterior obtendríamos la del área del rectángulo.
Para calcular el área a partir de la longitud de la diagonal y del ángulo que forman las dos diagonales, se empleará:

Perímetro del rectángulo

El perímetro del rectángulo es la suma de sus cuatro lados. Como el rectángulo tiene los lados iguales dos a dos, su perímetro será el doble de la suma de dos lados contiguos (es decir, a y b).

Si partiésemos del área del rectángulo y uno de sus lados, con esta fórmula hallaríamos directamente el perímetro sin necesidad de obtener el otro lado:

Ejercicios resueltos
Ejercicio 1

Sea un rectángulo cuyos lados son iguales dos a dos de longitud a=3 cm y b=5 cm.
El área del rectángulo será el producto de los dos lados diferentes, es decir:
El área del rectángulo de lados a=3 cm y b=5 cm es de 15 cm2.
Ejercicio 2
Hallar el área de un rectángulo del que nos dicen que su diagonal mide 18,475 cm y que las dos diagonales forman un ángulo agudo de 60°.
Solución:

El área buscada es de 147,8 cm2.
Ejercicio 3

Sea un rectángulo cuyos lados son iguales dos a dos de longitud a=3 cm y b=5 cm.
Su perímetro será dos veces la suma de dos lados contiguos:
