En el tema anterior, trabajamos con potencias de 10, en tanto aquí, en las actividades anteriores hemos multiplicado diferentes números por sí mismos; es decir, hemos usado la segunda potencia que también se conoce como elevar un número al cuadrado, con bases de diferentes de diez. De la misma manera que usamos la segunda potencia, podríamos generalizar y usar la n-ésima potencia utilizando cualquier número x como base. Por ejemplo, elevamos el número 5 a la séptima potencia de esta forma:

5⁷ = 5 x 5 x 5 x 5 x 5 x 5 x 5 = 78 125

1. Potenciación

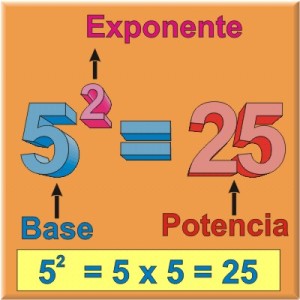
En la potenciación se distinguen los siguientes términos:

• Base: Factor que se repite.

• Exponente: indica el número de veces que se repite la base como factor.

• Potencia: es el producto que resulta de multiplicar la base por sí misma tantas veces como lo indique el exponente (producto de factores iguales). 

2. Radicación

Es la operación inversa de la potenciación.  

Llamamos raíz n-ésima de un número dado a al número b que elevado a n nos da a.

En la radicación se distinguen los siguientes términos:

• Radicando: Es el número al que se calcula su raíz.
• Índice: Es el número que indica la raíz que se extrae. Cuando el índice es 2, no es necesario escribirlo.
• Raíz: es el resultado de efectuar la operación.
• Radical: es el símbolo de raíz.

3. Raíz cuadrada

Para entender las raíces cuadradas primero tienes que entender los cuadrados…

¿Cómo calcular el cuadrado de un número?

Para calcular el cuadrado de un número, sólo hay que multiplicarlo por sí mismo…

EJEMPLO

¿Cuál es el cuadrado de 5?

Nota: escribimos “5 al cuadrado” cómo 5² (el “²” pequeño significa que el número aparece dos veces en la multiplicación)

La raíz cuadrada va en la dirección contraria:

5 al cuadrado es 25, así que la raíz cuadrada de 25 es 5

Se llama raíz cuadrada a la operación inversa de elevar un número al cuadrado. Extraer la raíz cuadrada de un número consiste en hallar otro número que elevado al cuadrado dé el número con que se empezó la operación.

4. Cuadrados perfectos o raíz cuadrada exacta

Los números 1, 4, 9, 16, 25, 36, 49, 64, y 81, son los cuadrados de los números 1, 2, 3, 4, 5, 6, 7, 8, y 9, respectivamente. Es interesante recordarlos porque son los únicos inferiores a 100 que tienen por raíz cuadrada un número entero. Estos números se denominan cuadrados perfectos. A partir de 100, los cuadrados perfectos son menos frecuentes.

5. Si un número no es cuadrado perfecto

6. Regla para el cálculo de la raíz cuadrada

7. Cómo calcular el cuadrado de números negativos

El cuadrado de 5  es 25: 5 x 5 = 25

Pero el cuadrado de – 5 también es 25: – 5 × – 5 = 25 (porque negativo por negativo es positivo)

¡Hay una respuesta positiva y otra negativa para una raíz cuadrada!

Así que la raíz cuadrada de 25 puede ser 5 o -5. Esto le pasa a todas las raíces cuadradas de números positivos.

Los números negativos no tienen raíz cuadrada porque no hay ningún número negativo que elevado al cuadrado (con exponente impar, sí) tenga como resultado un número negativo: un número negativo elevado al cuadrado da siempre positivo. Fíjate en este otro ejemplo:

√4 = 2, √4 = -2 pues 2² = ( – 2² ) = 4