Tema 5: Fuerzas equilibradas
Para mi proyecto
Página 138
Fuerza Normal
Si un cuerpo está apoyado sobre una superficie rígida, la acción de su peso debería hacer que se hundiese en ella, sin embargo esto generalmente no es así. Entonces, ¿Por qué no se hunde?. La lógica y el principio fundamental de Newton, nos dicen que debe existir alguna fuerza que anule el peso del cuerpo y permita mantenerlo en reposo. Esa fuerza, recibe el nombre de fuerza normal, reacción normal o simplemente normal, N.
La fuerza normal, reacción normal o simplemente normal (N) es una fuerza que ejerce una superficie sobre un cuerpo que se encuentra apoyado en ella. Su dirección es perpendicular a la superficie de apoyo y su sentido es hacia afuera.
¿Cómo calcular la fuerza normal?
La fuerza normal no tiene una expresión general a partir de la cual podemos calcular directamente su valor, sin embargo se puede deducir para cada caso de estudio haciendo uso del principio fundamental o segunda ley de Newton.
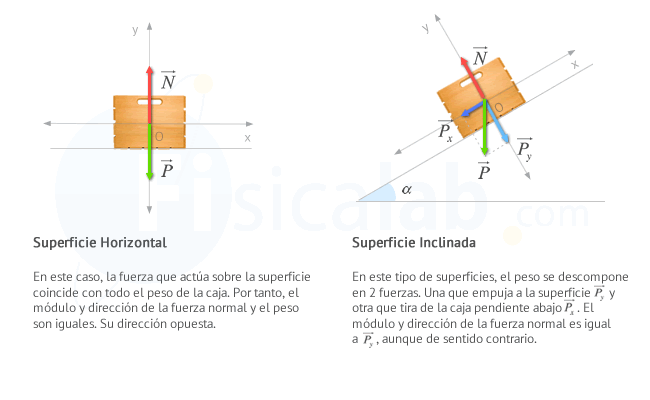
Fuerza normal de un cuerpo sobre una superficie horizontal.
Si el cuerpo no se hunde no hay aceleración en el eje y (verticalmente) y por tanto, si calculamos la fuerza resultante en este caso en concreto, obtenemos que:
∑Fy=m·ay ⇒N-P=m·0 ⇒N=P ⇒N=m·g
Fuerza normal de un cuerpo sobre una superficie inclinada.
En el caso de que el objeto se encuentre en una superficie inclinada que forma un ángulo α con la horizontal, el peso del cuerpo no se aplica completamente sobre la superficie. Si observas la figura, el efecto del peso se puede descomponer en una fuerza paralela al plano (Px→) y otra perpendicular (Py→). Px→ es la encargada de empujar el cuerpo pendiente abajo y Py→ de empujar a la superficie. Dado que la fuerza normal es la reacción a la fuerza que se ejerce sobre la superficie, el módulo y dirección de msubmsub→ será igual que Py→. Aplicando la descomposición de fuerzas estudiada en un apartado anterior, podemos calcular que:
Px=P·sinαPy=P·cosα
Como el cuerpo no se mueve a lo largo del eje y, su aceleración ay=0 m/s2. Teniendo en cuenta esto, si calculamos la fuerza resultante en este caso:
∑Fy=m·ay ⇒N-Py=m·0 ⇒N=Py ⇒N=m·g·cos(α)Experimenta y Aprendeα (rad) = 0.40m (kg) = 0.25αP→yP→xP→N→
Datos
P = m · g = 0.25 · 9.8 = 2.45 N
Px = P · sin(α) = 2.45 · sin(0.40) = 0.95 N
Py = P · cos(α) = 2.45 · cos(0.40) = 2.26 N
N = Py = 2.26 NFuerza normal
Arrastra los deslizadores para cambiar el peso del cuerpo (P) y el ángulo de inclinación (α) del plano que aparece en la figura.
Comprueba que:
- Si cambias el valor de la masa, provocarás un cambio en todas las fuerzas, ya que todas dependen directa o indirectamente de ella.
- Al cambiar el ángulo del plano, todas las fuerzas, excepto el peso cambiarán.
- Observa que a medida que aumentas el ángulo, se produce un efecto en cadena: Px se hace mayor (la parte del peso que hará que el cuerpo se deslice hacia abajo), Py menor (la fuerza que empuja a la superficie) y como se aplica menos fuerza sobre la superficie disminuye la fuerza normal.
Recuerda, la fuerza normal no es la fuerza de reacción al peso, sino a la fuerza que ejerce el cuerpo sobre la superficie sobre la que se apoya.
