Tema 4: Ecuación de la recta
Ecuación de la recta |
(Segundo medio)
Para entrar en esta materia y para entender lo que significa la Ecuación de la Recta es imprescindible estudiar, o al menos revisar, lo referido a Geometría analítica y Plano cartesiano .
La idea de línea recta es uno de los conceptos intuitivos de la Geometría (como son también el punto y el plano ).
La recta se puede entender como un conjunto infinito de puntos alineados en una única dirección. Vista en un plano, una recta puede ser horizontal, vertical o diagonal (inclinada a la izquierda o a la derecha).
 |
La línea de la derecha podemos verla, pero a partir de los datos que nos entrega la misma línea (par de coordenadas para A y par de coordenadas para B en el plano cartesiano) es que podemos encontrar una expresión algebraica (una función) que determine a esa misma recta.
El nombre que recibe la expresión algebraica (función) que determine a una recta dada se denomina Ecuación de la Recta .
Para comprender este proceder es como si la misma línea solo se cambia de ropa para que sepan de su existencia pero expresada en términos matemáticos (como una ecuación).
Es en este contexto que la Geometría analítica nos enseña que una recta es la representación gráfica de una expresión algebraica (función) o ecuación lineal de primer grado .
Esta ecuación de la recta varía su formulación de acuerdo con los datos que se conozcan de la línea recta que se quiere representar algebraicamente. Dicho en otras palabras, hay varias formas de representar la ecuación de la recta.
1.– Ecuación general de la recta
Esta es una de las formas de representar la ecuación de la recta.
De acuerdo a uno de los postulados de la Geometría Euclidiana, para determinar una línea recta sólo es necesario conocer dos puntos (A y B) de un plano (en un plano cartesiano) , con abscisas (x) y ordenadas (y) .
| Recuerden que es imprescindible dominar todos los aspectos sobre el Plano cartesiano pues la Ecuación de la recta no tiene existencia conceptual sin un Plano cartesiano. |
Ahora bien, conocidos esos dos puntos, todas las rectas del plano, sin excepción, quedan incluidas en la ecuación
Ax + By + C = 0
Que también puede escribirse como
ax + by + c = 0
y que se conoce como: la ecuación general de la línea recta, como lo afirma el siguiente:
|
Teorema La ecuación general de primer grado Ax + By + C = 0 , donde A, B, C pertenecen a los números reales ( |
2.– Ecuación principal de la recta
Esta es otra de las formas de representar la ecuación de la recta.
Pero antes de entrar en la ecuación principal de la recta conviene recordar lo siguiente:
Cada punto (x, y) que pertenece a una recta se puede representar en un sistema de coordenadas, siendo x el valor de la abscisa (horizontal) e y el valor de la ordenada (vertical).
(x, y) = (Abscisa , Ordenada)
Ejemplo: El punto (–3, 5) tiene por abscisa –3 y por ordenada 5.
Si un par de valores (x, y) pertenece a la recta, se dice que ese punto satisface la ecuación.
Ejemplo: El punto ( 7, 2 ) (el 7 en la abscisa x y el 2 en la ordenada y ) satisface la ecuación y = x – 5 , ya que al reemplazar queda
2 = 7 – 5 lo que resulta verdadero.
Recordado lo anterior, veamos ahora la ecuación de la recta que pasa solo por un punto conocido y cuya pendiente (de la recta) también se conoce , que se obtiene con la fórmula
y = mx + n
que considera las siguientes variables: un punto ( x, y ), la pendiente ( m ) y el punto de intercepción en la ordenada ( n ), y es conocida como ecuación principal de la recta (conocida también como forma simplificada, como veremos luego).
Al representar la ecuación de la recta en su forma principal vemos que aparecieron dos nuevas variables: la m y la n , esto agrega a nuestra ecuación de la recta dos nuevos elementos que deben considerase al analizar o representar una recta: la pendiente (m) y el punto de intercepción (n) (también llamado intercepto ) en el eje de las ordenadas (y) .
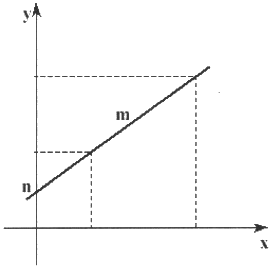 |
Respecto a esto, en el gráfico de arriba, m representa la pendiente de la recta y permite obtener su grado de inclinación (en relación a la horizontal o abscisa), y n es el coeficiente de posición, el número que señala el punto donde la recta interceptará al eje de las ordenadas (y).
Ver: Pendiente de la recta (positiva o negativa)
Forma simplificada de la ecuación de la recta
Si se conoce la pendiente m , y el punto donde la recta corta al eje de ordenadas es ( 0, b ) (corresponde a n en la fórmula principal ya vista), podemos deducir, partiendo de la ecuación de la recta de la forma
y − y 1 = m(x − x 1 )
y – b = m(x – 0)
y – b = mx
y = mx + b
Esta es una segunda forma de la ecuación principal de la recta (se la llama también forma explícita de la ecuación ) y se utiliza cuando se conocen la pendiente y la ordenada al origen (o intercepto), que llamaremos b ( no olvidemos que corresponde a la n en la primera forma de la ecuación principal). También se puede utilizar esta ecuación para conocer la pendiente y la ordenada al origen a partir de una ecuación dada.
Ejemplo: La ecuación y = 4x + 7 tiene pendiente 4 y coeficiente de posición 7, lo cual indica que interceptará al eje y en el punto (0, 7) .
Conocida la fórmula de la ecuación principal (simplificada o explícita, como quieran llamarla) de la recta es posible obtener la ecuación de cualquier recta siempre que se nos den al menos dos variables de ella: puede ser la pendiente, puede ser un punto o puede ser el intercepto.
Esto significa que si te dan esa información se puede conseguir una ecuación de la forma y = mx + b que cumple con esas condiciones dadas. Nótese que la ecuación y = mx + b es la forma generalizada de la forma principal y = mx + n; por lo tanto, la b corresponde al valor de n (el intercepto en la ordenada y ).
Ejemplo 1:
Hallar la ecuación de la recta que tiene pendiente m = 3 e intercepto b = 10 .
Tenemos que hallar la ecuación de la recta, esto es, y = mx + b .
Usamos la información que tenemos:
m = 3 y b = 10 y sustituimos en la ecuación
y = 3x + 10 .
La ecuación que se pide es y = 3x + 10 .
Nótese que esta forma principal (simplificada o explícita) también podemos expresarla como una ecuación general:
y – 3x – 10 = 0 , la cual amplificamos por –1, quedando como
– y + 3x + 10 = 0 , que luego ordenamos, para quedar
3x – y + 10 = 0
Ejemplo 2
Hallar la ecuación de la recta que pasa por el punto (1, 2) y tiene pendiente m = – 5 .
Tenemos que hallar la ecuación de la recta, esto es, y = mx + b .
Usamos a información: m = – 5 y sustituimos en la ecuación:
y = – 5x + b
Ahora tenemos que buscar la b ; usamos el otro dato; la recta pasa por el punto (1, 2) , por lo tanto, ese punto es una solución de la ecuación que buscamos. Se sustituyen esos valores de x = 1, y = 2 en la ecuación que estamos buscando: 2 = – 5 (1) + b
Despejamos la variable b en:
2 = – 5 (1) + b
2 = – 5 + b
2 + 5 = b
b = 7
Sustituimos el valor de b en la ecuación que buscamos: y = – 5x + 7
La ecuación en su forma principal (simplificada o explícita) es y = – 5x + 7 .
La cual también podemos expresar en su forma general:
y = – 5x + 7
y + 5x – 7 = 0
la cual ordenamos y queda
5x + y – 7 = 0
Pendiente de una Recta
Con respecto a la pendiente es necesario conocer los siguientes enunciados:
Las rectas paralelas tienen la misma pendiente.
Si una recta tiene pendiente m = – 3 y es paralela a otra, entonces esa otra también tiene pendiente m = – 3.
Las rectas perpendiculares tienen pendientes recíprocas y opuestas.
Si una recta tiene pendiente m = – 5 y es perpendicular a otra, entonces esa otra tiene pendiente 1/5.
Además:
Si m = 0 la recta es horizontal (paralela al eje x). Si y = 0 , la recta es perpendicular. Si n = 0 la recta pasa por el origen.
Determinar la pendiente
Aprendido lo anterior es muy fácil hallar la ecuación de la recta que pasa por un punto y tiene una pendiente dada, o para hallar la ecuación de la recta que pasa por dos puntos.
Si nos dicen, por ejemplo, que una recta tiene una pendiente de 2 y que pasa por el punto ( 1, 3 ), sólo tenemos que sustituir estos valores en la ecuación principal y nos quedaría:
3 = 2 · 1 + n,
y despejando n , queda n = 1 .
Por lo tanto, la ecuación de esa recta será:
y = 2x + 1 .
Si nos dicen que la recta pasa por el punto ( 1, 3 ) y ( 2, 5 ), sólo tenemos que sustituir estos valores en la ecuación principal y obtendremos dos ecuaciones con dos incógnitas:
3 = m · 1 + n,
5 = m · 2 + n.
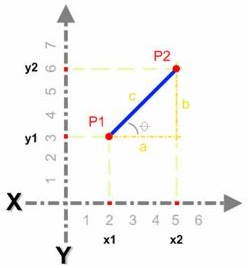 |
Ahora, observemos el gráfico de arriba: Cuando se tienen dos puntos de una recta P 1 (x 1 , y 1 ) y P 2 (x 2 , y 2 ) , la pendiente, que es siempre constante , queda determinada por el cuociente entre la diferencia de las ordenadas de esos dos puntos y la diferencia de las abscisas de los mismos puntos, o sea, con la fórmula
![]()
Entonces, a partir de esta fórmula de la pendiente se puede también obtener la ecuación de la recta, con la fórmula:
y – y 1 = m(x – x 1 )
Esta forma de obtener la ecuación de una recta se suele utilizar cuando se conocen su pendiente y las coordenadas de uno solo de sus puntos.
Entonces, la ecuación de la recta que pasa por el punto P 1 = (x 1 , y 1 ) y tiene la pendiente dada m, se establece de la siguiente manera:
y – y 1 = m(x – x 1 )
Ejemplo
Hallar la ecuación de la recta que pasa por el punto A (2, – 4) y que tiene una pendiente de – 1/3
Al sustituir los datos en la ecuación, resulta lo siguiente:
y – y 1 = m(x – x 1 )
y – (–4) = – 1/3(x – 2)
3(y + 4) = –1(x – 2)
3y + 12 = –x + 2
3y +12 + x – 2 = 0
3y + x + 10 = 0
x + 3y + 10 = 0
Volviendo a la ecuación general de la recta (Ax + By + C = 0) , en ella la pendiente ( m ) y el coeficiente de posición ( n ) quedan determinados por:
![]()
![]()
Ejemplo: ¿Cuál es la pendiente y el coeficiente de posición de la recta 4x – 6y + 3 = 0 ?
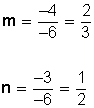
Ecuación de la recta que pasa por dos puntos
Sean P(x 1 , y 1 ) y Q(x 2 , y 2 ) dos puntos de una recta. Sobre la base de estos dos puntos conocidos de una recta, es posible determinar su ecuación.
Para ello tomemos un tercer punto R(x, y) , también perteneciente a la recta.
Como P, Q y R pertenecen a la misma recta, se tiene que PQ y PR deben tener la misma pendiente. O sea
![]() y
y ![]()
Luego, la ecuación de la recta que pasa por dos puntos es:
![]()
que también se puede expresar como
![]()
Ejemplo 1:
Determina la ecuación general de la recta que pasa por los puntos P(1, 2) y Q(3, 4)
![]()
![]()
![]()
y – 2 = x – 1
y – 2 – x + 1 = 0
y – x – 2 + 1 = 0
y – x – 1 = 0
Ejemplo 2:
Determina la ecuación general de la recta que pasa por los puntos P 1 (4, 3) y P 2 (–3, –2)
Sabemos que la ecuación de la recta que pasa por dos puntos es:
![]()
Reemplazamos los valores:
–2 – 3 = y – 3
–3 – 4 x – 4
–5 = y – 3
–7 x – 4
y – 3 = x – 4 (–5 /–7)
y – 3 = –5 x + 20
–7
–7 (y – 3) = –5 x + 20
–7y +21 + 5x – 20 = 0
5x – 7y + 1 = 0
Que se corresponde con una ecuación de la forma general
Ax + By + C = 0
Donde
A = 5
B = 7
C = 1
Ecuación de la recta dados punto–pendiente (se conoce un punto y se conoce la pendiente)
Por lo ya visto, y por los ejemplos anteriores, sabemos que la ecuación de la recta que pasa por dos puntos está determinada por
![]()
pero
![]()
Luego, si reemplazamos en la ecuación anterior obtenemos
![]()
despejando, llegamos a:
y – y 1 = m(x – x 1 )
Ejemplo:
Determina la ecuación general de la recta de pendiente –4 y que pasa por el punto (5, –3)
y – y 1 = m(x – x 1 )
y – (–3) = –4(x – 5)
y + 3 = –4x + 20
y = –4x + 20 –3
y = –4x +17
Luego la ecuación pedida es 4x + y – 17 = 0 .
Ejercicios para obtener la ecuación general de la recta dados un punto y la pendiente
Recuerde que la fórmula inicial es y – y 1 = m(x – x 1 )
1. m = –1; punto (–2, 3)
y – 3 = –1(x + 2)
y – 3 = –x – 2
x + y – 1 = 0
2. m = 2; punto (–3/2, –1)
y + 1 = 2(x + 3/2)
y + 1 = 2x + 3
– 2x + y – 2 = 0
2x – y + 2 = 0
3. m = 0; punto (–3, 0)
y – 0 = 0(x + 3)
y = 0
4. m= –4; punto (2/3, –2)
y + 2 = –4(x – 2/3)
y + 2 = –4x + 8/3
y +2 – 4x –8/3 = 0
y – 2/3 – 4x = 0
4x – y + 2/3 = 0
5. m = 1; punto (1,4)
y – 4 = 1(x – 1)
y – 4 = x – 1
y – 4 – x + 1 = 0
y – 3 – x = 0
x – y + 3 = 0
6. m = 3/4; punto (2,5, –3)
y + 3 = ¾(x – 2,5)
y + 3 = 3/4x – 15/8
y + 3 – 3/4x +15/8 = 0
y + 39/8 – 3/4x = 0
3/4x – y – 39/8 = 0
7. m = ind; punto (0,5)
y – 5 = (x – 5)
y – 5 – x + 5 = 0
y – x = 0
x – y = 0
8. m = 0; punto (–4, 1/2)
y – ½ = (x + 4)
y – ½ – x – 4 = 0
y – 9/2 – x = 0
x – y + 9/2 = 0
