Tema 6: Triángulos rectángulos y cálculo de la hipotenusa.
DEFINICIÓN DETRIÁNGULO RECTÁNGULO
Los triángulos son polígonos que cuentan con tres lados. Cabe recordar que los polígonos son figuras planas, delimitadas por segmentos (es decir, por sus lados). El triángulo, por lo tanto, es una figura plana formada por tres segmentos.
Cuando un triángulo dispone de un ángulo recto (que mide noventa grados), se lo clasifica como un triángulo rectángulo. Los otros dos ángulos del triángulo rectángulo siempre son agudos (miden menos de noventa grados).
El ángulo recto en el triángulo rectángulo está formado por los dos lados de menor longitud, conocidos como catetos, mientras que el tercer lado (el de mayor extensión) recibe el nombre de hipotenusa. Las propiedades de estos triángulos señalan que la longitud de la hipotenusa siempre resulta menor que la suma de los catetos. La hipotenusa, por otra parte, siempre es más extensa que cualquiera de los dos catetos.
El famoso teorema de Pitágoras se basa en estas características de los triángulos rectángulos y señala que el cuadrado de la hipotenusa resulta idéntico al resultado de la suma de los cuadrados de los dos catetos.
De este modo, se establece la siguiente ecuación para todo triángulo rectángulo:
Hipotenusa al cuadrado = Cateto al cuadrado + Cateto al cuadrado
Cabe destacar que los triángulos rectángulos pueden ser triángulos isósceles (los dos catetos tienen la misma extensión: es decir, son iguales) o triángulos escalenos (la extensión de cada lado es diferente a las de los dos restantes).
Por otra parte, si deseamos calcular el área de un triángulo rectángulo, podemos apelar a la siguiente fórmula:
Área = (Cateto x Cateto) / 2
Como puede apreciarse, uno de los puntos fundamentales de los triángulos es las relaciones que podemos establecer entre sus diferentes lados y ángulos, algo que resulta esencial para resolver un gran número de problemas, tanto en el campo de las matemáticas como en muchos otros. Antes de continuar con dichas relaciones, es necesario cubrir otro tema: la proyección ortogonal.
La proyección ortogonal pertenece al ámbito de la geometría euclidiana, la cual estudia las propiedades geométricas de los espacios en los cuales se cumplen los axiomas de Euclides, un grupo de proposiciones consideradas evidentes que pueden generar otras a través de deducciones lógicas. Para realizar una proyección ortogonal son necesarios dos elementos: un conjunto de puntos (que puede estar compuesto por uno solo); una recta de proyección. El primero se proyecta sobre la recta con ayuda de líneas auxiliares perpendiculares a ésta, de manera que las dimensiones resultantes sólo son correctas en un caso: cuando se proyecta un segmento paralelo a la recta.
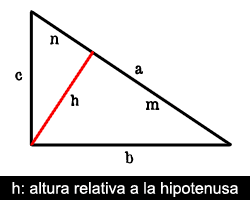
Este concepto se utiliza a menudo en el desarrollo de videojuegos para crear una falsa sensación de profundidad, ya que no importa la distancia de los objetos con respecto a la cámara: siempre tendrán las mismas dimensiones en pantalla. Ahora bien, si proyectamos de esta forma los catetos sobre la hipotenusa, obtenemos una media geométrica denominada altura relativa a la hipotenusa, un segmento que parte del punto en el que se encuentran ambos catetos y corta la hipotenusa de forma perpendicular.
Cuando trazamos la altura relativa a la hipotenusa, el triángulo rectángulo se convierte en tres triángulos: el original más los dos que contiene (según se observa en la imagen). Esto da lugar a ciertas relaciones métricas. Por ejemplo, la suma de ambas proyecciones es igual a la hipotenusa (a = m + n). También es correcto decir que el producto de las dos proyecciones es igual al cuadrado de la hipotenusa, ya que h/m = n/h, y si despejamos h nos da hh = mn.
El producto entre la proyección de un cateto y la hipotenusa es igual al cuadrado de dicho cateto: b/a = m/b => bb = am. Por último, el producto de los catetos es igual a la altura relativa multiplicada por la hipotenusa: a/c = b/h => ah = bc.
