Tema 5: Modelar situaciones usando las funciones lineales.
Modelación matemática de situaciones cotidianas mediante funciones lineales
Lo que necesitas saber para esta lección
Antes de iniciar esta lección, debes revisar la lección sobre Problemas verbales que involucran ecuaciones y funciones lineales.
Lo que aprenderás en esta lección
En esta lección aprenderás a aplicar las funciones lineales en la resolución de situaciones cotidianas.
Modelación matemática
Las situaciones cotidianas que involucran la relación entre magnitudes, se pueden representar de diversas formas utilizando algunos modelos matemáticos. Entre estos modelos se encuentran las funciones lineales.A continuación, vamos a presentar algunas situaciones que se expresan mediante funciones lineales en sus diversas representaciones gráficas, verbales o simbólicas.
Situación 1
Francisco tiene una tienda de productos para fiestas infantiles. En su tienda, él vende globos que encierran un regalo dentro, como se observa en la figura:

Globo osoCada globo de este tipo cuesta 202020 dólares. Si xxx es la cantidad de globos y FFF es el monto que se paga por dicha cantidad de globos,¿qué expresión algebraica relaciona correctamente estas variables? y ¿cuál es la representación gráfica de esta relación?[Quiero ver la explicación de este problema]
Situación 2
La empresa de telefonía celular ALÓ, proporciona una nueva oferta.
- Un pago fijo de 303030 dólares mensuales, que incluye 150150150 minutos para llamadas.
- Se cobrará 0.200.200, point, 20 dólares por cada minuto adicional a los 150150150 minutos incluidos en el pago de 303030 dólares.
Muestra una representación gráfica de la función que representa el pago (en dólares) por xxx minutos de llamadas.[Quiero ver la explicación de este problema. ]
Situación 3
Claudia construye figuras geométricas usando palitos de madera del mismo tamaño. Para cada lado del triángulo equilátero utiliza un palito. Las figuras que construye las ubica en fila, como se observa en la figura:
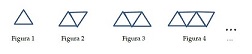
grafico palitosa) Su compañero Julio afirma: “En la figura 4, Claudia ha usado 9 palitos de madera, entonces, por regla de tres simple, en la figura 8 usará el doble; o sea 18 palitos de madera”.a) ¿La proposición expresada por Julio es verdadera o falsa? ¿Por qué?[Quiero ver la explicación de este apartado.]b) Encuentra una expresión algebraica que permita obtener el número de palitos que tendrá la figura “n” de la secuencia.[Quiero ver la explicación de este apartado.]c)¿Cuántos palitos de madera usaría Claudia al construir la figura 548548548? ¿Por qué?[Quiero ver la explicación de este apartado.]d) Determina qué lugar en la fila ocuparía la figura que construya Claudia con exactamente 675675675 palitos de madera.[Quiero ver la explicación de este apartado.]e) Representa en el plano cartesiano la función obtenida en (b). Ten en cuenta el dominio de esa función.[Quiero ver la explicación de este apartado.]
Situación 4
El gasto en la cantidad xxx de insumos de la empresa \text {A}Astart text, A, end text se calcula usando la función:f(x)=\dfrac{9}{4} x + 20f(x)=49x+20f, left parenthesis, x, right parenthesis, equals, start fraction, 9, divided by, 4, end fraction, x, plus, 20.En cambio, la empresa \text {B}Bstart text, B, end text gasta sus insumos según la función:g(x)=\dfrac{4}{3}x + 50g(x)=34x+50g, left parenthesis, x, right parenthesis, equals, start fraction, 4, divided by, 3, end fraction, x, plus, 50.a)¿En cuál de las empresas el crecimiento del gasto es más “lento”?[Quiero ver la explicación de este apartado]b)¿Es verdad que si cada una de las empresas compra más de 323232 unidades de insumos, la empresa \text {A}Astart text, A, end text gasta menos que la empresa \text {B}Bstart text, B, end text?
