Tema 6: Líneas rectas y curvas

Líneas rectas y curvas

Hace muchos, muchos años (unos 2.000 más o menos) hubo una cultura a la que debemos una parte importante de las matemáticas tal y como las conocemos hoy: la Antigua Grecia. Probablemente la aportación más importante fue la de Euclides, que recopiló todo lo que se sabía hasta el momento de matemáticas y lo unió en un conjunto de libros, Los Elementos. Y no solo lo recopiló y ordenó sino que también lo ordenó “lógicamente”, es decir, creó un sistema que ordenaba los contenidos según sus implicaciones lógicas (el razonamiento deductivo). Así nacieron los axiomas, los teoremas… (un axioma lleva a un teorema) ¿Te imaginas lo importante que fue esto? Es difícil de imaginar…

Euclides dedicó gran parte de sus libros a la geometría (¡a los griegos les encantaba!), de hecho, en este apartado su obra perduró intacta hasta el siglo XIX (pero eso ya pertenece a las matemáticas avanzadas). Así que lo que estudiamos hoy en el colegio de geometría se escribió ¡hace más de dos mil años!

El post de hoy lo vamos a dedicar a estudiar las líneas rectas y las líneas curvas tal y como las estudió él.

Hay muchas maneras de definir las líneas rectas y curvas, la más extendida (y que puedes encontrar en este post sobre líneas rectas y líneas curvas que escribimos hace meses en el blog) es la siguiente:

• Una línea recta es una sucesión de puntos alineados en una misma dirección. Es decir, que para ir de un punto a otro nunca cambiamos la dirección.
• Por el contrario, los puntos de una línea curva sí cambian de dirección para ir de uno a otro.

Lo podemos ver con el siguiente dibujo: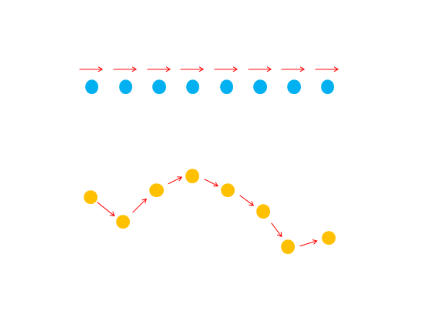

¡Pero esta no es la única forma de hacerlo! La forma original (y a que se utiliza hoy en día en matemáticas) es más parecida a la que utilizó Euclides. Piensa en dos puntos encima de un papel. ¿De cuántas maneras puedes llegar desde uno hasta otro?

Si no hay obstáculos podemos llegar de muchísimas formas… por ejemplo:

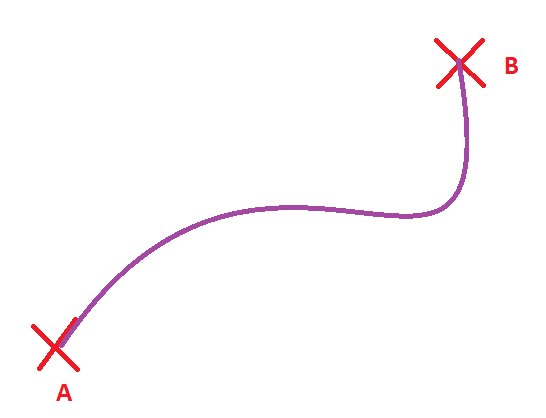
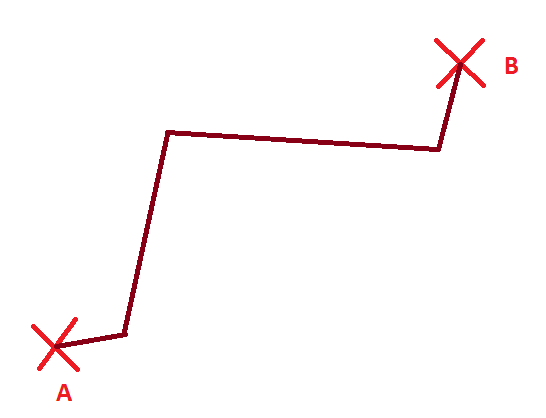
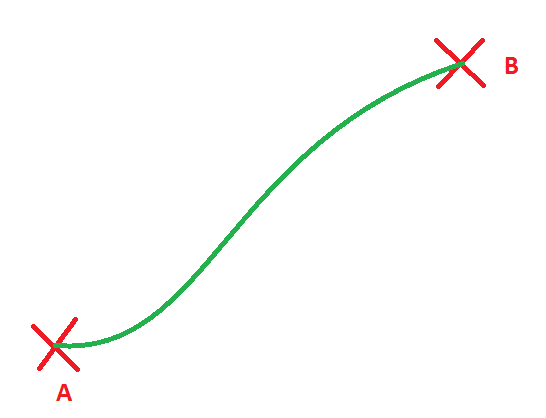
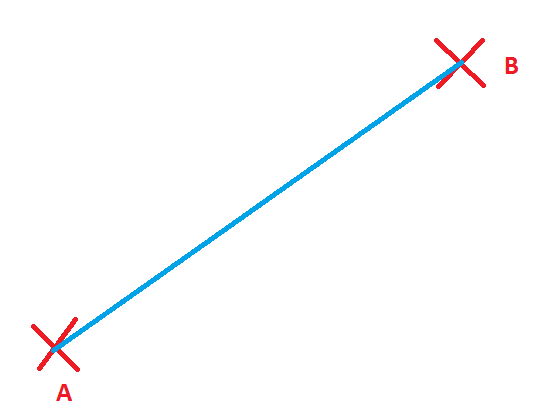
¡Y muchas más! ¿Verdad? Ahora la pregunta clave, ¿qué línea, de entre todas las que podemos dibujar, es la más corta? Es decir, ¿cuál es el camino más corto que va de A hasta B? ¡Eso es! La última línea, la azul. Así definimos la línea recta.

Entre dos puntos, la línea que los une es recta si es el camino más corto entre ellos.

Si no es el camino más corto, entonces es una línea curva.

¡Espera! ¿Qué pasa con la segunda línea que hemos dibujado? Este es un caso especial, porque decimos que no es una sino varias líneas.

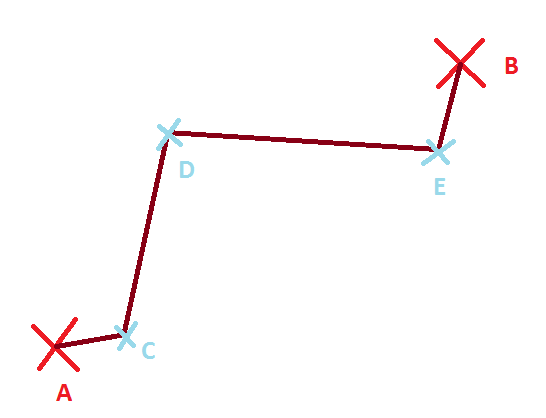
• La que une A con C
• La que une C con D
• La que une D con E
• La que une E con B

Así que nos falta saber lo que es una línea… ¿cómo sabemos si tenemos una o varias líneas? Este  es un tema un poco más complicado, pero voy a intentar que lo entiendas.

En general, decimos que una línea no puede tener esquinas (lo que en matemáticas llamamos derivable). Si encontramos una línea con una esquina, quiere decir que no es una sino varias líneas. En nuestro caso, tenemos 3 esquinas

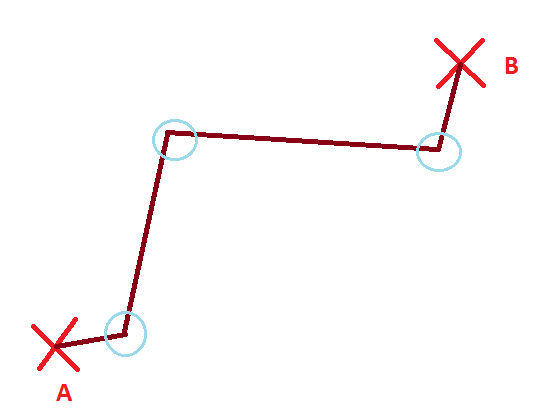
Entonces podemos dividir lo que habíamos dicho al principio que era una línea en varias, que ya no nos valen para “la línea que une A con B”, ¡porque no es una!

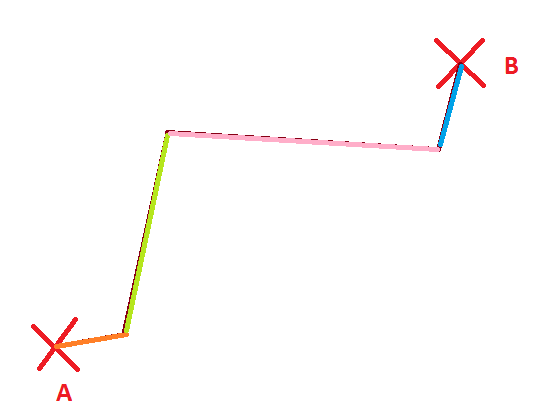
¿Cuántas líneas rectas crees que puedes dibujar entre A y B? Una, ¿verdad? ¡Y líneas curvas muchas! Euclides y todos los que le siguieron pensaron lo mismo durante mucho, mucho tiempo. Hasta que en el siglo XIX llegó un señor que se llamaba Gauss que pensó… ¿y qué pasa si los puntos A y B los pongo encima de una esfera? Por ejemplo, un avión que va desde  Madrid hasta el Melbourne no puede seguir una línea recta (a no ser que hagamos un túnel), entonces ¿qué camino toma? Y lo más importante, ¿hay algún otro?