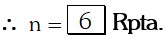Tema 5: Criterios de divisibilidad 2, 3, 4, 5, 6, 9 y 10.
Sabías que…
Página 22
NÚMEROS PRIMOS
Aquí te compartiremos todas las formulas, ejemplos, ejercicios resueltos y ejercicios para resolver del tema de Números Primos puedes revisar nuestroíndice de contenido para que navegues con mas facilidad en este contenido.
Introducción a los Números Primos
En este capítulo estudiaremos los números primos que desde la antigüedad a interesado a grandes matemáticos como (Gauss, Fermat, Euler, …,etc.) siendo el matemático Griego Euclides el primero en descubrir los números primos y el reto actual de los matemáticos es encontrar la fórmula que permita encontrar todos los números primos lo cual no a sido posible hasta el momento pero hoy en día se ha encontrado números primos más grandes gracias a la memoria de las grandes súper computadoras, siendo los últimos números primos:
- 2199337 – 1 que tiene 6002 cifras (en el año 1971).
- 2217001 – 1 que tiene 6511 cifras (en el año 1979).
- 2859433 – 1 que tiene 258716 cifras (en el año 1994).
- 26972593 – 1 que tiene más de dos millones de cifras (en el año 1999).
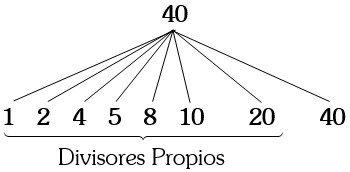
Para esto es necesario recordar que Divisor de un número es cualquier valor que lo divide en partes enteras como por ejemplo los divisores del número 40 son: 1; 2; 4; 5; 8; 10; 20 y 40.
Divisor Propio:
Es todo aquel divisor del número menor que dicho número, tomando el ejemplo anterior diremos que los divisores de 40 son:
Clasificación de los Números Según sus Divisores
Números Primos
Llamados también números primos absolutos; número primo es aquel número que tiene dos divisores únicamente: la unidad y el mismo.
Ejemplo:

Tabla de Números Primos Menores que 200

Observación:
- No existe fórmula para hallar los números primos.
- La serie de los números primos es infinita.
- El único número primo par es el 2, entonces los demás son impares.
- Si “P” es un número primo mayor que 2 cumple ser 4° ± 1.
- Si “P” es un número primo mayor que 3 cumple ser 6° ± 1.
Números Compuestos
Se llama número compuesto a todo número que tenga más de dos divisores. Esta serie es más abundante e infinita. Como por ejemplo:

Números Primos Entre Si o Primos Relativos (PESI)
Se dice que dos o más números son primos entre sí, solo si tienen un único divisor común que siempre es la unidad.
Ejemplo:

Como vemos en el ejemplo el único divisor común que tienen los números 15 y 16 es la unidad por consiguiente estos números son primos entre sí o primos relativos.
NOTA:
El número uno NO es primo NI compuesto, por que sólo tiene un solo divisor que es el mismo es un número SIMPLE.
Regla para Determinar la Primalidad de un Número Entero Positivo
- Primero se extrae la raíz cuadrada aproximadamente del número N.
- Luego se toma todos los números primos menores a esta raíz cuadrada de N.
- En seguida se comprueba si estos números primos lo dividen al número N.
- Si ningún número primo lo divide en cantidad entera y exacta al número N se dice que éste número es Primo.
- Si algún número primo lo divide al número N, se dice que éste número es Compuesto.
Ejemplo:
Determinar si 149 es un número primo.
Solución:
Primero extraemos la raíz cuadra al número en mención:
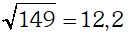
Los números primos menores a esta raíz cuadrada son:

- Dividimos 149 entre todos ellos:

- Como vemos que ninguno lo divide exactamente, entonces podemos decir que 149 es un número primo!!
Estudio de los Divisores de un Número
Descomposición Canónica de un Número o Descomposición del Número en sus Factores Primos
(Teorema Fundamental de la Aritmética o Teorema de Gauss)
Todo número entero mayor que uno se puede descomponer como el producto de sus factores primos elevados a exponentes enteros positivos y dicha descomposición es única.
Ejemplo:

Tabla de Divisores de el Número 1800:
- Primero hallamos todas la potencias consecutivas del 2 y luego estos resultados colocamos a la cabeza de la tabla:
- En seguida hallamos las potencias del 3 y del 5 empezando con el exponente 1 y colocamos estos resultados en columna.
Luego multiplicamos todos los factores del 3 con los factores del 5 y colocamos en seguida (también en columna).

Entonces los divisores del número 1800 son todos los valores que están a la derecha de la línea vertical.
Cantidad de los Divisores de un Número
Para hallar la cantidad de los divisores de un número (CD(N)) primero se descompone a los números en sus factores primos
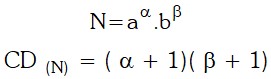
Ejemplo:
Halla la cantidad de divisores del número 20.
Solución:
Descomponemos el número 20 = 22.5
Luego aplicamos la formula anteriormente mencionada:

La cantidad de divisores del número 20 es 6 Rpta.
Cantidad de Divisores Compuestos de un Número
Para hallar la cantidad de divisores compuestos de un número N, se resuelve con la fórmula:

Ejemplo:
Hallar la cantidad de divisores compuestos del número 400.
Solución:
Primero descomponemos el número 400 = 24.52
Para hallar la cantidad de divisores primos bastará fijarnos en las bases de la descomposición; entonces los divisores primos del 400 son 2 y 5; por lo tanto tiene dos divisores primos.
Entonces aplicamos en la fórmula:

La cantidad de divisores compuestos del número 400 es 12 Rpta.
Suma de los Divisores de un Número
Para hallar la cantidad de los divisores de un número (SD(N)) primero se descompone a los números en sus factores primos.

Ejemplo:
Halla la suma de los divisores del número 20.
Solución:
Descomponemos el número 20 = 22.5
Luego aplicamos la formula anteriormente mencionada:

La suma de los divisores del número 20 es 42 Rpta.
Producto de los Divisores de un Número
Para hallar el producto de los divisores de un número (PD(N)); primero se necesita hallar la cantidad de los divisores del número CD(N); la fórmula que nos permite encontrar el producto de divisores es:

Ejemplo:
Halla el producto de los divisores del número 20.
Solución:
Descomponemos el número 20 = 22.5
Primero hallamos la cantidad de divisores del número 20:

Luego para hallar el producto de los divisores del número 20, reemplazamos en la formula que te mencionamos con anterioridad:

El producto de los divisores del número 20 es 203 Rpta.
Suma de las Inversas de los Divisores de un Número
Para hallar la suma de las inversas de los divisores de un número (SID(N)), primero se tiene que hallar la suma de los divisores del número SD(N); la fórmula que nos permite a encontrar la suma de las inversas de los divisores del número es:
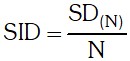
Ejemplo:
Halla la suma de las inversas de los divisores de 20.
Solución:
Descomponemos el número 20 = 22.5
Primero hallamos la suma de los divisores del número 20:

Luego para hallar la suma de las inversas de los divisores del número 20, reemplazamos en la formula que te mencionamos con anterioridad:
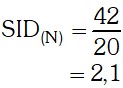
La suma de las inversas de los divisores del número 20 es 2,1 Rpta.
Indicador de un Número o Función Euler
Llamado también Función Euler “∅ (N)”, nos indica cuantos números menores o iguales a un número N son primos entre sí con él.
Primero se descompone al número en sus factores primos:
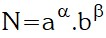
Luego se aplica la siguiente fórmula:

Ejemplo:
Hallar cuantos números menores que 500 son primos entre sí con él.
Solución:

Entonces el número 500 tiene 200 números menores que él que son primos entre sí con él.
Cantidad de Formas Posibles en que un Número N se puede Expresar como el Producto de Dos Números Enteros
La cantidad de formas posibles en que un número N se puede expresar como el producto de dos números enteros, se da por la fórmula:
Si la cantidad de divisores es par:

Si la cantidad de divisores es impar:

Ejemplo:
De cuantas formas diferentes 40 se puede expresar como el producto de dos números enteros.
Solución:
Primero hallamos la cantidad de divisores de 40:

Luego reemplazamos en la fórmula:

Complementos Teóricos
Número Perfecto:
Es aquel número que es igual a la suma de sus divisores propios.
Ejemplo:
El número 6 es perfecto por que la suma de sus divisores propios es 6:

Número Defectuoso:
Es aquel número cuya suma de divisores propios es menor que el número.
Ejemplo:
El número 4 es un número defectuoso por que sus divisores propios son: 1 y 2; y la suma de estos divisores es: 1+2=3; y este resultado es menor que 4.
Número Abundante:
Es aquel número cuya suma de divisores propios es mayor que el número.
Ejemplo:
El número 12 es un número abundante por que sus divisores propios son: 1; 2; 3; 4; 6; y la suma de estos divisores es: 1+2+3+4+6=16 y este resultado es mayor que 12.
Números Amigos:
Dos números son amigos cuando la suma de los divisores propios de uno es igual al otro número y viceversa:
Ejemplo:
Los números 284 y 220 son números amigos por que:

Números Saturados:
Son aquellos números con la mayor cantidad posible de divisores que cualquier otro número menor que él.
Ejemplo 01:
El número 24 es un número saturado por que la cantidad de divisores que tiene es 8 y ningún otro número menor que él tiene más divisores que dicho valor.
Ejemplo 02:
El número 360 es un número saturado por que la cantidad de divisores que tiene es 24 y ningún otro número menor que él tiene más divisores que dicho valor.
Ejemplos de Números Primos
Ahora veremos algunos ejemplos de números primos.
Ejemplo 01:
Hallar “x” si: N=6×162x tiene 40 divisores
Solución:
Realizamos la descomposición de N:

Hallamos la cantidad de divisores:

Teniendo como dato: CD(N)=40, reemplazando:

Por identificación de factores

Ejemplo 02:
Hallar el valor de “n” sabiendo que: 15n x 75 tiene (17n+34) divisores.
Solución:
Realizamos la descomposición de la expresión:

Hallamos la cantidad de divisores:

Teniendo como dato: CD(N)=17n+34, reemplazando:

Por identificación de factores:
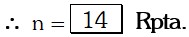
Ejemplo 03:
¿Cuántos ceros debe tener N=2000…00 para que el resultado tenga 56 divisores?
Solución:
Sea:

Realizamos la descomposición de la expresión:

Teniendo como dato: CD(N)=56, reemplazando:

Por identificación de factores